Chapter 1: Molecular Orbital Concepts

A. Concepts of MO Theory.

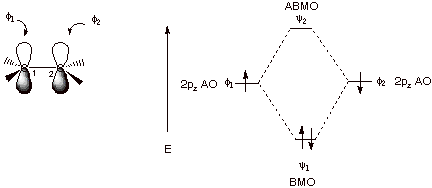
1. Strong Covalent Bonds. Consider the pi bond of ethene in simple molecular orbital terms (The qualitative results would be the same for any pi or sigma bond.

q The overlap of the two atomic orbitals (AO’s) results in the formation of two molecular orbitals (MO’s), one of which is lower in energy than the original AO’s (the bonding MO or BMO) and the other higher in energy than the original AO’s (the antibonding MO or ABMO).

q Two paired electrons can occupy the lower energy MO, resulting in pi bond formation.

q The fundamental requirements for strong bond formation are:

o Efficient overlap

o Two paired electrons.

2. Weak Covalent Bonding.

a. One electron bonding. If only one electron is present, it can occupy the BMO, also resulting in significant bonding, but since there is only one electron to contribute to the bonding, the bonding is not nearly as strong as in the case of two electron bonding.

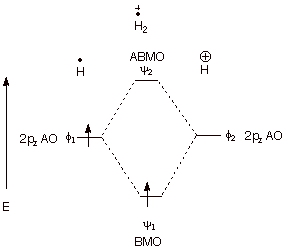
q The hydrogen molecule positive ion. Consider the combination of a proton and a hydrogen atom. This results in the formation of H₂ with just one electron (it is a cation radical). The bonding energy of this species is actually fairly impressive, being measured as 64 kcal/mol.

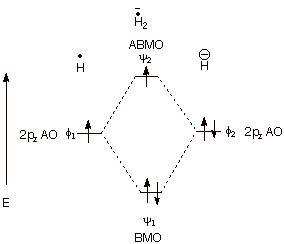
b. Three Electron Bonding. Consider the combination of a hydrogen atom (one electron) with a hydride anion (two electrons). In this case the third electron must go into the ABMO, thus negating some of the bonding energy derived from the BMO. However, there are two electrons contributing to bonding, and just one electron to antibonding. Consequently, there is net, albeit, relatively weak three electron bonding.

q Three electron bonding is an important means of stabilizing some radical species. Consider the methoxymethyl radical shown below. A 2p_z AO on carbon (the radical site) overlaps with a 2p_z AO on oxygen which contains an unshared pair of electrons. Overlap between the two 2p_z AO’s results in the formation of MO’s, which are populated by three electrons, as shown.

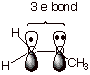
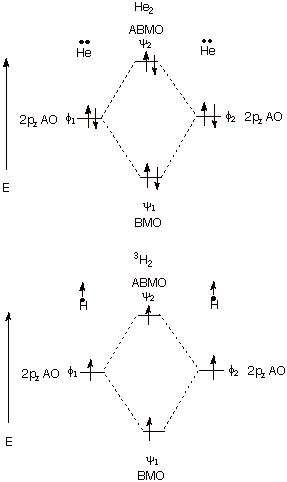
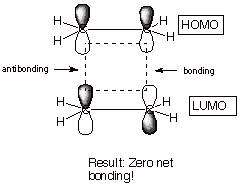
3. Zero Net Bonding. When there are zero or four electrons present or when there are two electrons which are unpaired, no net bonding results. Since the energy we are discussing is electronic energy, when there are no electrons present, there is obviously no bonding energy. The four electron no-bond case is nicely illustrated by dihelium, which has almost exactly zero bonding. The bonding provided by two electrons in the BMO is cancelled to an excellent approximation by the antibonding engendered by two electrons in the ABMO. The case of two unpaired electrons is illustrated by the triplet state of dihydrogen. Both the dihelium (4 e) and dihydrogen triplet (two unpaired electrons) cases are illustrated below. In the latter case, the second electron cannot enter the BMO because off Pauli Exclusion.

B. The MO’s and Their Energies.

We want to have a slightly closer look at the pi MO’s of ethene and their energies. The approximation we use is an extremely simplified one known as the Huckel MO or HMO approach. The approach neglects the sigma electrons, considering only the pi electrons , and approximates the MO’s as linear combinations of the atomic orbitals (the LCAO approximation).

1. The LCAO-MO Approximation for the Pi System of Ethene.

The pi MO’s of ethene are assumed to have the somewhat general form given below, where the a’s represent the numerical coefficients of the two AO’s. Since there are two MO’s, the subscript i is used to write a general form for both of these MO’s (where i is 1 for the BMO and 2 for the ABMO (i.e., numbering from the MO of least energy to the highest). The coefficients have two subscripts, since potentially each atom may have a different coefficient in each MO. Thus a₁₁ is the coefficient of atom 1 in MO 1, a₁₂ is the coefficient of atom two in MO1, a₂₁ is the coefficient of atom 1 in MO 2, etc. Essentially, theses coefficients, a_ij, give the weight of the 2p_z AO of atom 1 or 2 in MO i.

The relative magnitudes of the coefficients can be found from symmetry arguments (they must have the same absolute magnitude, i.e., equal or opposite, because C1 is equivalent to C2) or by Variationally minimizing the energy with respect to the coefficients (not considered here). The absolute values of the coefficients are found by imposing the normalization condition, i.e., when integrated the square of the wave function gives the value one, corresponding to a total electron density of one. Using symmetry, we can see that one of the MO’s (the BMO) has equal coefficients (here set to 1) and the other opposite coefficients (set to 1 and –1). These are shown as “primed” wave functions. When normalized (subject also to the condition of the neglect of the overlap integral, which is usually employed in the HMO method), the final form of the MO’s is obtained (shown as unprimed wave functions).

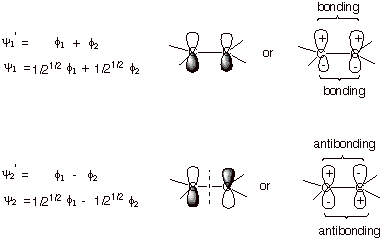
q Note that in the BMO, the bonding corresponds to positive overlap on both faces of the molecule, while in the ABMO, antibonding results from negative overlap. Positive overlap occurs when both overlapping lobes have the same sign (both plus or both minus). As a result, the MO accrues additional electron density in the region between the two carbon atoms, which corresponds to the main bonding region. In the ABMO, the subtraction of the AO’s results in less electron density in the bonding region.

2. Energies of the MO’s.

The energies of the MO’s can be obtained by solving the HMO secular determinant. In the HMO approximation, they are expressed in terms of the parameters a and b. The former is called the coulomb integral and roughly corresponds to the energy of an electron in the 2p AO of one of the carbons (no covalent bonding). The second parameters is called a resonance integral, and corresponds to the stabilization resulting from overlap and bonding (covalent pi bonding). An energy level diagram of these orbitals and their energy is illustrated below.

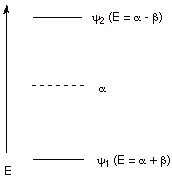
q Since both parameters are negative (they correspond to stabilization or lowering in energy), the plus sign corresponds to the BMO and the minus sign to the ABMO.

q The pi bonding for each electron in ethene is thus b, so that for the two electorn bond the molecular bonding energy is 2b.

q The a part of the energy corresponds to the stabilization the electron would have on the atom itself, without covalent bonding or overlap, so although it contributes to the atomic binding (the binding of the electron to its nucleus), it doesn’t contribute to the covalent bonding in the pi bond.

C. Antibonding MO’s.

In ethene, only the BMO is occupied; the ABMO is vacant. It contributes nothing to the energy of the system. It is sometimes described as a virtual MO. The question sometimes arises of what use is the concept of an ABMO or of any virtual orbital. Essentially it is that the presence of this MO reminds us of the ability of the molecule to accept an electron into this orbital in the context of a reaction. There are two principal ways in which the ABMO ceases to be a virtual orbital and becomes a real, occupied MO.

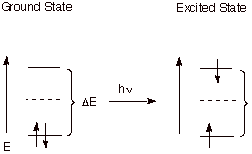
1. Excited States.

When a molecule absorbs radiation which satisfies the Einstein equation dE = hn, it promotes an electron from the BMO to the ABMO. This excited state of the original molecule is highly energetic and capable of undergoing potentially useful chemistry (photochemistry) which the more stable ground state is incapable of.

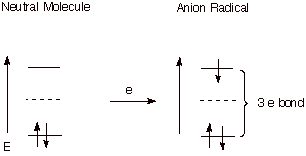
2. Anion Radicals

In the context of purely thermal chemistry, as opposed to photochemistry, electrons may be transferred from an electron rich species ( called a single electron donor) to a neutral molecule to form a negatively charged species which also has an unpaired electron in the ABMO. These species are called anion radicals. Again, they have an electron in a relatively high energy antibonding orbital, so they are much more reactive, in general than the original neutral molecule. They, in fact, are excellent representatives of species having a three electron bond. Since the electron in the antibonding orbital diminishes the pi bonding present in the molecule, the species is highly reactive. Electron donors suitable for transferring electrons to ABMO’s of neutral molecules include alkali metals, negative electrodes, and some electron rich organic molecules.

The energy required to introduce an electron into the ABMO of a neutral molecule in solution is called the reduction potential. The higher the energy of the ABMO into which the electron must be introduced, the more negative the potential needed for the electron transfer. Reduction potentials as typically measured are relative, not absolute, and are typically referred to the saturated calomel electrode (SCE). In general, two structural factors are especially important in lowering the energy of the appropriate ABMO and thus the reduction potential of a substrate molecule (i.e., making it easier to reduce). First, the more extended the conjugated system, the lower the energy of the ABMO and the more easily reducible the substrate. Second, pi bonds which have strongly electron-withdrawing groups attached, which can stabilize the negative charge of the anion radical, also have lower energy ABMO’s. One of the more easily reducible organic substrates is tetracyanoethylene. The anion radical of this substrate is so stable that its salts can be isolated. A detailed single crystal neutron diffraction study of one such salt reveals the distribution of the odd electron and thus the shape of the ABMO. Interestingly, the AO’s on the central carbons are bent back, away from one another, in order to minimize overlap, which is negative, antibonding overlap. The knowledge of theshapes of ABMO’s comes in handy in several connections which we will be considering further on. Incidentally, the MO which has the single electron is often referred to as the SOMO (singly occupied MO). This orbital is especially important because it determines where the odd electron is and also, largely, the negative charge.

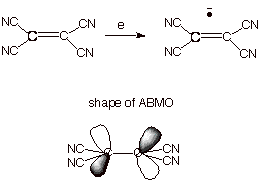
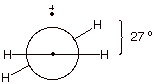
D. Cation Radicals and One Electron Bonds.

Cation radicals are reactive organic species which can be formed by removing an electron from an occupied MO of a neutral molecule. The pi bond in such a system is an excellent example of a one electron bond. Nevertheless, these species are highly reactive, since they do not have the typical strong two electron bond. The weakening of the pi bond in the ethene cation radical is reflected in the structure of this species which, unlike ethene, is twisted by ca. 27^o out of planarity.

E. Allylic conjugation.

1. MO’s of the Allyl System (Radical, Cation, and Anion).

The allyl system is a three carbon system in which the carbon atoms are all sp² hybridized, and the trigonal planes are all coincident, so that the unhybridized 2p_zAO’s are all “parallel” and undergoing efficient pi overlap. Since all three atoms are involved

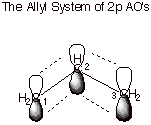
in the pi overlapping, the MO’s are delocalized over three atoms, rather than the more usual two atoms as exemplified in the pi bond of ethene. A conjugated pi system is one which, like the allyl system, has the electrons shared by more than two atoms. We will not invoke the mathematical coefficients of the MO’s, but will use the simple qualitative depiction of them shown below in order to understand the electron distribution in the MO’s and the energies of the MO’s.

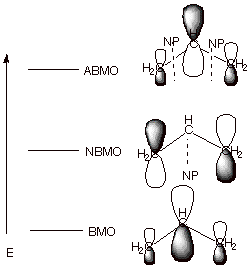
q First, since there were now three 2p_z AO’s in the basis set, there are three MO’s which result from their combination by overlap. Only one MO is bonding, and there is an antibonding and a nonbonding MO. A nonbonding MO (NBMO) is one which has the same energy as the basis set AO, i.e., has not benefit from delocalization.

q The BMO has a larger coefficient at C2 (the central carbon) than at C1 and C3, corresponding to a larger electron density at C2 in this particular orbital. Note also that all overlaps are positive and bonding, corresponding to a relatively lower energy MO.

q The NBMO, in contrast, has the largest coefficients at C1 and C32 (the terminal atoms), and a zero coefficient at C2 (there is a nodal plane, NP, through C2, where the coefficient changes sign from positive to negative. Note that there is no overlap between neighboring atoms, e.g., C1-C2 or C2-C3, because the coefficient at C2 is zero (zero electron density). This corresponds to the circumstance that this MO is nonbonding.

q The ABMO returns to the general shape of the BMO, in the sense that the largest coefficient is at the central atom. The high energy of this MO corresponds to the circumstance that all neighboring group overlaps are negative and antibonding.

q Note that, the most bonding MO in a conjugated system is always fully bonding, i.e., has no negative overlaps and no nodal planes. The next MO in terms of increasing energy has one nodal plane, and so on. The energy increases monotonically with the number of NP’s because these correspond to nonbonding or antibonding interactions.

2. The Pi Bonding Energy and Delocalization Energy of the Allyl Carbocation.

The allyl carbocation has 2 pi electrons, as may be seen by examining a canonical structure of the ion. The double bond of the latter contributes 2 pi electrons, while the

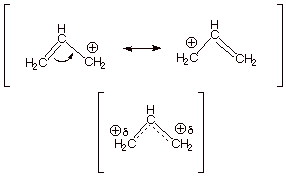
carbocation center has a vacant 2p_z AO and contributes zero electrons. The energy level diagram is therefore as shown below. Note that the total pi electron energy is more negative (more bonding) than the two electrons of the ethene pi bond, by 0.82b. This is the delocalization energy, i.e., the additional stabilization of these two electrons derived from their delocalization over three atoms, instead of just two. Formally, the key to the lowering of the energy is the lower energy of the BMO in the allyl system than in the ethene system.

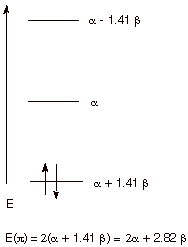
We might also note, that since the BMO is heavily concentrated on the central carbon atom, most of the electron density of the allyl cation is located at C2. Therefore, the positive charge is at C1 and C3as typical resonance structures of the allyl cation indicate. If one calculates the electron densities, it is found that, in precise agreement with the resonance theory, there is exactly zero positive charge on the central carbon and exactly one-half unit of positive charge on each of the terminal atoms. As shown in the diagram below, the contribution to the electron density at a specific atom from a single electron in the BMO is given by the square of the coefficient of that atom in the BMO. For atoms 1 and 3, that is 1/4; for atom 2 it is 1/2. Since there are two electrons in

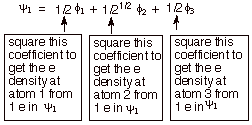
this MO, we must double this, giving 1/2 for C1 and C3 and 1.0 for C2. To be neutral, each carbon should have exactly 1.0 2p_z electrons, so the net charge at C2 is zero, and at C1 and C3 it is +1/2. We can formalize this procedure as follows, where q is the total pi electron density at atom i , Q_i is the charge density at atom i (1-q_i), N_i is the number of electrons in a given orbital (the occupancy number), a_ij is the coefficient of atom i in the jth MO, and the summation is over all singly or double occupied orbitals (since each occupied MO contributes something to the electron density). In the simple case of the allyl cation, there is only one occupied orbital, so no summation is required.

As an exercise, use this formala to calculate the charge densities at C1, C2, and C3 in the allyl cation, radical, and anion. The radical, as we will see, has 3 electrons, and the anion has 4. As a further exercise, see if you can calculate the spin distribution in the radical, assuming that all of the electron spin comes from the singly occupied MO (the SOMO). Then compare these results with the results of applying simple resonance theory to the cation , radical, and anion.

F. Conjugated Dienes.

1. Energy Levels and Delocalization Energy of 1,3-Butadiene.

The simplest conjugated diene, 1,3-butadiene, has a conjugated system in which the pi electrons are delocalized over four carbon atoms. The energy levels are show in the diagram below. Since there are four basis set AO’s, there are four MO’s, two of them bonding and two antibonding. Note the symmetrical disposition of the MO’s about the nonbonding level. As an exercise, fill in the appropriate number of electrons and calculate the pi electron energy and delocalization energy of this system. The appropriate comparison, for the purposes of calculating the DE is with two ethene molecules.

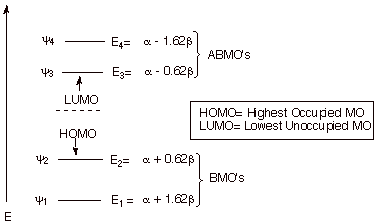
2. Electron Densities, and Charge Densities in Butadiene.

As an exercise, use the previously given formula to calculate the q_i’s and Q_i’s for neutral butadiene. By symmetry, of course, the results for C1 and C4 are identical, as are those for C2 and C3. Are the results physically reasonable?

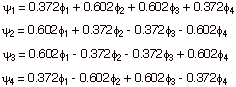
Note that not only are the energies of the first and fourth MO’s related by symmetry, these MO’s have coefficients which are identical in absolute values. Similarly, the coefficients of the second and third MO’s are closely related. Again, also note that the first MO has zero nodes, the second has one, the third two, and the fourth three.

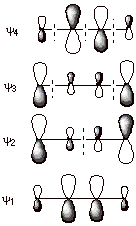
3. Ion Radicals of Butadiene.

The cation radical of butadiene is formed when one electron is removed from neutral butadiene. As an exercise, construct the energy level diagram of butadiene cation radical. Assuming that all of the charge and spin arise from the singly occupied MO (SOMO; a good approximation), calculate the charge(Q_i) and spin (r_I) at each carbon atom (again, you may use symmetry considerations, i.e., C1 = C4 and C2 = C3)). Do the same for the butadiene anion radical, which has one additional electron (five) compared to neutral butadiene. Compare the charge and spin densities in the anion and cation radicals. If the anion radical were to be protonated, where would it be likely to react? Write an equation for this reaction. Similarly, if the cation radical were to react with a nucleophile such as hydroxide ion, where would it react. Draw the equation for this reaction, also.

G. Longer, Acyclic Conjugated Systems; Generalizations

1. Even Number of Carbon Atoms

The next higher conjugated system having an even number of carbon atoms in it would be a conjugated triene, such as 1,3,5-hexatriene. You should anticipate by now that with six carbon atoms there would be six pi MO’s, three of which would be bonding and three antibonding. The antiboding MO’s would each be paired with a BMO, in terms of symmetry about the nonbonding level. The number of nodes would increase in the sequence 0,1,2,3,4,5 in order of the increasing energies of the MO’s. Since the LUMO of butadiene was considerably lower in energy than that of ethene, you could also expect that a continued increase in the length of the conjugated system would continue to drop the energy of the triene LUMO and correspondingly increase the energy of its paired HOMO.

As an exercise, draw out the energy level diagram for a triene system and compare it with the corresponding diene system.

2. Odd Number of Carbon Atoms.

Just as the allyl system had an odd number of carbon atoms (three) in the conjugated system, there are also conjugated systems having 5,7, etc. carbon atoms in them. The pentadienyl system is the simplest of these. The main difference between these

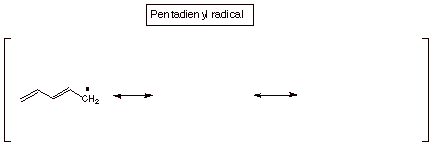
odd carbon systems and the even carbon ones is that the odd carbon systems (which can have, like the allyl system, a carbocation, a radical, and an anion) have a NBMO. Like the allyl radical, the pentadienyl radical has its odd electron in the NBMO, so we only need to know the coefficients of the NBMO in order to predict the odd electron density in this radical, or for that matter the positive charge density in the carbocation and the negative charge density in the carbanion. Incidentally, this latter circumstance may be somewhat non-intuitive. The radical, which has 1 electron in the NBMO is, as a hydrocarbon radical would be expected to be, nonpolar, i.e., it has zero charge on every atom. So, if one adds one electron to form theanion, it is added to the NBMO and the results is that the negative charge is determined by the distribution of this electron in the NBMO. Similiarly, if one electron is removed from the radical to generate the carbocation, it is removed from the NBMO, so the positive charge is generated at the positions determined by the electron density in the NBMO.

As an exercise, consult Streitweiser and Coulson’s Dictionary of Pi Electron Calculations in the Chemistry Library to find the coefficients of the pentadienyl system. Use these to calculate the spin distribution in the pentadienyl radical and the charge distributions in the cation and anion. Compare these with the results predicted from resonance theory (i.e., write the three resonance structures for the radical, carbocation and anion).

H. MO’s of Cyclic, Conjugated Systems.

1. The Cyclopropenyl System. Cyclic conjugated systems such as cyclopropenyl, cyclobutadiene, benzene, etc. have higher degrees of symmetry than acyclic systems. For example, benzene has a six-fold symmetry axis, whereas acyclic systems generally have no more than a two-fold symmetry axis. One result of this is that cyclic conjugated systems typically have a number of degenerate orbitals, i.e., MO’s of the same energy but having different spatial distributions of the electrons. The simplest cyclic conjugated system, cyclopropenyl, has one pair of degenerate MO’s which are antibonding. The display of MO’s is shown below. Note that there is one very highly bonding MO, along with the degenerate pair. In contrast to allyl, there is no NBMO. With only a single BMO, this conjugated system is best adapted to accommodate two electrons, i.e., as a carbocation. In the cyclopropenyl radical (three electrons) , one electron is forced to occupy a high energy ABMO, and in the anion (four electrons), two electrons must be filled into the ABMO’s. Recall that in the acyclic, allyl case, the cation, radical, and anion are all relatively stable, since the electrons entering the NBMO do not diminish the stabilization. The total pi electron energy of the cyclopropenyl cation is seen to be much lower than that of the allyl cation. However, the corresponding four electron anion has less stabilization than the allyl anion, and no more than a simple double bond of ethene.

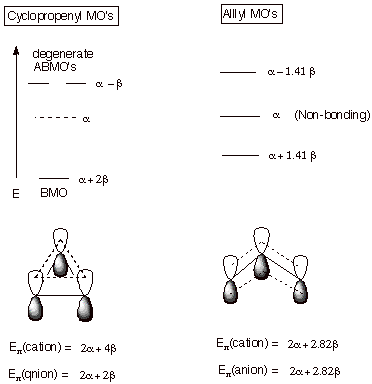
2. The Circle Mnemonic. A good way to recall the distribution of MO’s in simple monocyclic conjugated systems is to use the circle mnemonic. According to this mnemonic device, a polygon of the appropriate number of sides is inscribed inside a circle with one vertex down, corresponding to the unique, highly bonding MO. The MO’s then are arrayed at the vertices of the polygon. Examples for the cyclopropenyl and cyclopentadienyl systems are illustrated. Note that the cyclopentadienyl system now has three BMO’s, so it can accommodate six electrons (that would make this 5 carbon system an anion).

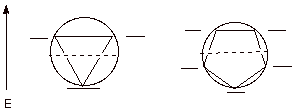
3. Cyclobutadiene. The molecule 1,3-cyclobutadiene has two equivalent resonance structures analogous to the Kekule structures of benzene. We will see, however, that cyclobutadiene could not be more different from benzene in its resonance stabilization and its stability. Following the circle mnemonic, you should be able to easily see that cyclobutadiene has only one BMO, like cyclopropenyl, and that the degenerate pair of MO’s is actually nonbonding. To be neutral, cylcobutadiene must have four pi electrons, but two of them would have to go into the nonbonding level and would add nothing to the pi bonding. Consequently, the pi electronic energy of this molecule is the same as two ethylene units, i.e., it has no resonance stabilization at all. This molecule is highly unstable, even at temperatures not far from absolute zero ( e.g., 20 K). From this we can see that the resonance treatment of cyclobutadiene (two equivalent resonance structures) failes to agree with the MO treatment or with experiment. The problem is that in cyclic systems, the electron count is of crucial importance, and the simple resonance treatement does not take this into account.

4. The Huckel Rule. As you may recall, the cyclic systems which have special stability can be predicted by the 4n+2 Rule, where n = 0,1,2,3---. Therefore, monocyclic conjugated systems having 2,6,10,14,---electrons are highly stabilized, but those having 4n electrons (4,8,12,---) are surprisingly lacking in stability, even in comparison to their acyclic counterparts. The basis for the Huckel Rule is essentially that the bonding MO’s of cyclic systems occur in a regular pattern. There is one highly bonding MO, followed by varying numbers of pairs of BMO’s (zero for cyclopropenyl, cyclobutadiene; two for cyclopentadiene, benzene, and cycloheptatriene, etc.). There will always be 1,3,5,7—BMO’s, which can accommodate 2,6,10,14 – electrons when completely filled.

5. Exercises.

a. Benzene. Construct a display of the MO’s of benzene and fill in the appropriate nujmber of electrons, using one canonical structure as a basis for computing the number of pi electrons. Using the information that the MO’s have energies a+2b,a+b,a+b,a-b,a-b, and a-2b , calculate the pi electron energy of benzene and compare it with the energy of three molecules of ethene. Estimate the resonance energy (delocalization energy) of benzene as the difference in pi electron energy of benzen and three ethene molecules.

b. 1,3-Cyclopentadiene and 1,3,5-cycloheptatriene. Construct energy level diagrams for these systems and fill in the appropriate numbers of electrons for the cation and anion of each. Which species are especially stable? Do these agree with the Huckel Rule.

6. Aromaticity./Antiaromaticity. The circumstance that the delocalization energy of cyclic conjugated systems crucially depends on the electron count, even more than on the number of carbon atoms over which the electrons are potentially delocalized gives rise to the Huckel Rule. The stability of such systems varies from the benzene standard (highly stabilized) to no stabilization whatsoever (or even destabilization). Systems which are unusually highly resonance stabilized, like benzene, the cyclopropenyl cation, the cyclopentadienyl anion, and the cycloheptatrienyl cation are often termed aromatic. Those which are regarded as especially unstable are often referred to as antiaromatic. The concept of aromaticity/antiaromaticity has come to have use in in the concept of transitions states and reaction rates. Not that a transition state is so stabilized as to be an energy minimum, of course, but that a TS which has a 4n+2 cyclic conjugated system is likely to be much lower in energy than a comparable one which has a 4n cyclic conjugated system. Let’s consider some examples of how the concept of aromaticity/antiaromaticity can be used in rationalizing relative reaction rates.

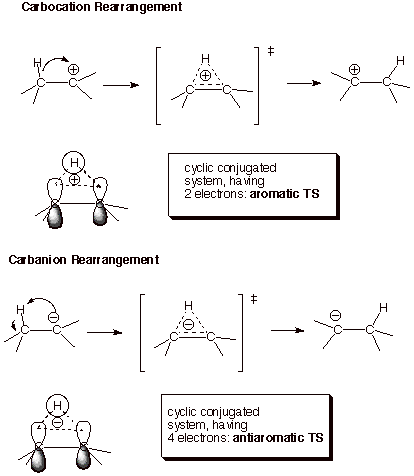
a. Carbocation vs Carbanion or Radical Rearrangements. It is well known that carbocations tend to rearrange very quickly to a more stable carbocation if one is available throught the 1,2 shift of a hydrogen, alkyl, or other group to the previous carbocation center. On the other hand, neither radicals nor anions rearrange to a more stable radical or anion by an analogous process. In fact, carbocations rearrange relatively rapidly even to an equally stable (not more stable carbocation). There is an obvious intrinsic preference for cationic over radical or anionic rearrangements, even when the thermodynamic driving force is factored out. What is the basis for such a strong preference for cationic rearrangement? One way of understanding this preference is based upon TS aromaticity/antiaromaticity. The rearrangement, in either case must take place via a TS which has the hydrogen (or other atom) bridging the migration origin and the migration terminus (the carbon from which it migrates and the carbocation or anion center to which it migrates). This creates a cyclic system of overlap in the TS, so that the electron count is critical. In the carbocation case, there are just two electrons (examine the reactant canonical structure; the two electrons are from the C-H bond which is being broken; the carbocation center, of course, has zero electrons). This TS is therefore aromatic. In contrast, the TS for the anionic rearrangement has four electrons 9the carbanion center contributes two, plus thus of the C-H bond), is is antiaromatic. The difference in the facilities of these two types of reaction is dramatic. Indicentally, the TS for a radical rearrangement has three electrons and is considered nonaromatic. These rearrangements are not observed to occur.

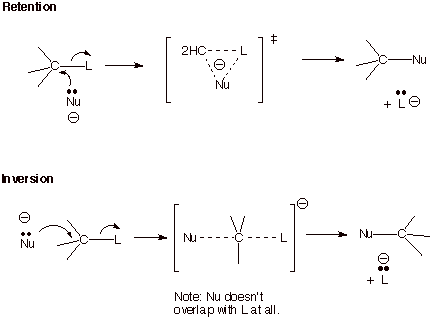
b. The Strong Preference for Inversion over Retention in S_N2 Reactions. From the diagram below, we can also see that an S_N2 reaction which occurs with retention of configuration at the carbon undergoing substitution (“frontside attack” of the nucleophile, Nu) has a cyclic conjugated system. If we count electrons, we can see that there are four electrons (two from the nucleophile and two from the C-L bond) in the cyclic TS, which is therefore antiaromatic and disfavored in comparison to the invertive process (“backside attack”, because the latter process is nonaromatic (it doesn’t have a cyclic conjugated system).

c. Cycloaddition. It is well known that the Diels-Alder reaction is one of the most facile and useful reactions in organic chemistry. It is no coincidence that the TS for this reaction has a cyclic system containing 6 electrons, i.e., an aromatic TS. In contrast, cycloadditions having 4 or 8 electrons are much more difficult to bring about.

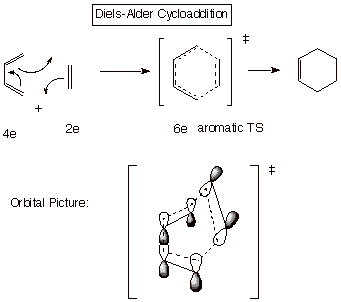
In sharp contrast, the cycloaddition between two alkene units, to give a cyclobutane is very difficult to achieve and typically does not occur in the concerted manner of the Diels-Alder reaction (one bond is formed at a time and high temperatures are usually required). A concerted mechanism would have a TS with antiaromatic character. As an exercise, see if you can draw a dotted line TS structure, such as that shown for the Diels-Alder reaction, for such a reaction.

The Diels-Alder reaction is said to be a [4+2} cycloaddition, because the diene component contributes 4 electrons and the dienophile 2 electrons to the cyclic conjugated system present in the TS. The reaction between two alkenes is termed a [2+2] cycloaddition.

Carbene Additions to Alkenes. The addition of carbene (CH₂) and substituted carbenes (like dichlorocarbene) to alkenes is an effective way of making cyclopropane and its derivatives. Singlet carbenes have an electron pair in a hybrid orbital and also a vacant 2p AO. In adding to the pi bond of ethene or any alkene, the mode of carbene addition to form two new C-C bonds is rather unique, but is correctly predicted by the concept of TS aromaticity. Note that an aromatic TS is set up when the carbene presents its vacant 2p AO to the face of the pi bond, giving a two electron cyclic TS. If the carbene presents the filled hybrid AO to the face of the pi bond, an antiaromatic, four electron cyclic TS is set up. The former is therefore strongly preferred over the latter. The especially interesting part is that by presenting the hybrid AO to the face of the pi bond, the methylene group would be oriented precisely the way it needs to be to form the product cyclopropane. However, when the vacant 2p AO is presented, the methylene hydrogens are far out of position in respect to where they will need to be in the product. What is the solution to this dilemma? Simply that the required rotation of the methylene group into the proper position takes place after the transition state, so that any undesirable antiaromatic effects are not felt in the TS and are overcome by the bonding which is very strong at that point. So the interesting thing about carbene additions is that the do not take place by the “Path of Least Motion.”

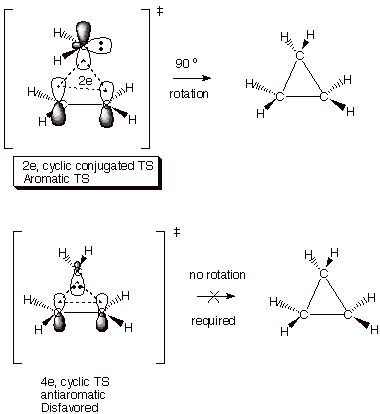
I. Frontier Orbital (FO) Theory and Perturbation Theory.

1. Filled/Vacant Interactions and HOMO/LUMO Interactions. We already understand that when two AO’s interact, as in the prototype case of the hydrogen molecule, two MO’s are formed, and if two paired electrons are available to enter the BMO, strong bonding results. The requirement for two electrons can be satisfied by having two electrons in one AO (this would be a hydride anion) and zero in the other (a proton), or by having two hydrogen atoms, each with one electron, with the electrons having opposite spin. An analogous situation arises when any two orbitals interact, even if the orbitals are MO’s, although the bonding which results may be much weaker than in the case of molecule formation from atoms. We have already seen that essentially all molecules (simple or complex) have filled bonding BMO’s and vacant antibonding MO’s. If two molecules come into contact, there is therefore always a possibility of bonding interactions between the two, since each molecule has filled MO’s and vacant MO’s. These interactions would result in “supermolecule” formation or complexation, in which the new MO’s are delocalized over the entire complex. In the case of interactions between molecules, the bonding interactions are sometimes modest and may be negated by repulsive nonbonding interactions between the molecules and the unfavorable entropy effect of combining two molecules into one complex molecule. In other cases, relatively stable complexes (e.g., pi complexes) may be formed.

q Any interaction between a filled and a vacant MO can potentially result in a stabilizing interaction because the filled orbital will be stabilized and the vacant one destabilized and two electrons are present, so that only the stabilized MO is occupied. These interactions will be referred to as filled/vacant interactions or F/V interactions.

q Note that interactions between two filled MO’s can also result in the formation of delocalized MO’s, but there will be no net stabilization because both the stabilized and destabilized MO’s are doubly occupied (the four electron situation).

q Similarly, the interactions between two vacant MO’s obviously results in no stabilization, although delocalized virtual MO’s may result.

q Importantly, although any of the potentially many F/V interactions may be stabilizing, the HOMO/LUMO interactions are virtually always the most important ones, because the interaction energy depends upon the energy difference between the F and V MO’s. In the case of the HOMO/LUMO interaction, this energy difference is obviously the smallest. The energy difference between a given HOMO and the corresponding LUMO of the other molecule is sometimes termed the “HOMO-LUMO gap”.

q The approximation in which only the HOMO/LUMO interaction is considered (among all of the possible F/V interactions) is called the Frontier Orbital (or FO) approximation.

2. Symmetry Effects.

In the case of interactions between molecules in which a cyclic conjugated system of orbitals is set up, there is an additional limitation placed upon the interacting F/V MO’s, viz., symmetry. Specifically, the interacting MO’s must have the same symmetry classification. Typically, the MO’s are classified as either symmetric (S) or antisymmetric (A) with respect to a symmetry element, e.g. a plane of symmetry which each interacting molecule has and which is also common to the complex formed between them.

q Antisymmetric means that when the symmetry operation is applied, the electron distribution is unchanged, but the coefficients of all of the orbitals change sign.

q Symmetric means that when the symmetry operation is applied, the electron distribution is unchanged and the coefficients of all of the orbitals remain as they were before the symmetry operation.

q The symmetry element can be almost any element, but most commonly is a plane of symmetry or an axis of symmetry.

q Note that the BMO of the pi bond of ethene is S with respect to a plane of symmetry (coefficients have the same magnitude and sign), but the ABMO is A, because the coefficients of the two carbons have the same absolute magnitude (meaning that when the wave function is squared to obtain the electron density, the electron density is the same at both carbons), but the coefficients of the two carbon atoms are opposite in sign. In the same way, by referring to the MO’s of the allyl system, you can see that the first MO is S, the second A, and the third S. In the butadiene system, the same pattern is followed, the lowest energy MO being S, the next A, the third S, and the highest energy MO A.

J Applications of FO Theory.

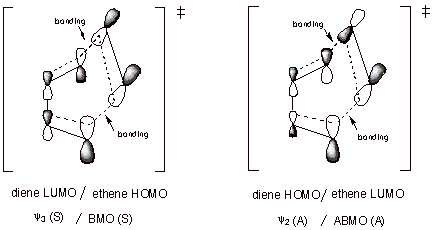
1. Diels-Alder TS. The TS for the Diels-Alder cycloaddition reaction can be considered as approximating a cyclic complex between butadiene (in the s-cis-conformation) and ethene. There are two non-equivalent HOMO/LUMO interactions as shown in the illustration below. In both cases, there is a symmetry match, so that the interactions occur and result in stabilization.

q The diene HOMO is the second MO, which is antisymmetric. The ethene LUMO is the ABMO, which is also antisymmetric. The interactions at both termini of the diene are bonding, so there is net bonding interaction.

q The diene LUMO is the third MO, which is symmetric. The ethene HOMO is the BMO, which is also symmetric. Again, the symmetry match provides that the interactions at both diene termini can simultaneously be bonding.

q Both HOMO/LUMO interactions contribute to the stabilization of this TS.

q The Diels-Alder reaction is an example of a [4+2] cycloaddition, in that the diene supplies 4 pi electrons to the cyclic TS, and ethene supplies 2.

2. [2 + 2] Cycloadditions. You canerify that in the attempted combination of two ethene molecules to give cyclobutane both HOMO?LUMO interactions are not symmetry matched. Although bonding can take place at one terminus, the interaction at the other terminus is antibonding, resulting in no net interaction.

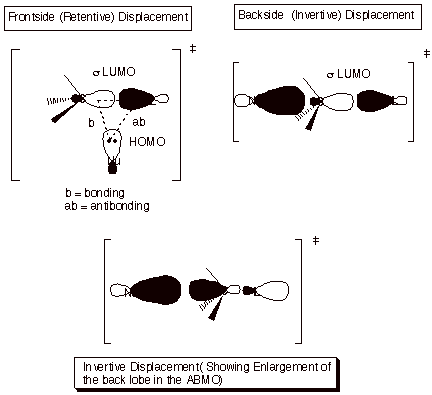
3. Inversion in an S_N2 Reaction

In the displacement of a leaving group by an entering nucleophile, the nucleophile N^-) obviously supplies the electron pair (the filled orbital). To obtain a stabilizing interaction, this orbital must overlap with a vacant orbital, not the filled bonding orbital of the C-L bond. The vacant orbital must then be the ABMO corresponding to the C-L sigma bond. Since the latter MO has a nodal plane between C and L, it is clear that in a purely hypothetical frrontside (retentive) displacement, the nucleophile cannot interact bondingly with carbon without simultaneously interacting antibondingly with L. However, it can interact bondingly with carbon from the backside, without significantly interacting with L.

There is another interesting part to this discussion. You might think that overlap with the small lobe of the sp³ orbital of carbon might be rather inefficient. However, as we had noted earlier in the case of the tetracyanoethene anion radical, the ABMO is attenuated in the bonding region and enlarged in the back lobe, so that overlap is actually enhanced from the back side when the sigma bond LUMO is involved.

CH 368 Terms and Concepts

Alternant Hydrocarbon System: A planar,conjugated pi electron system which contains no odd-membered rings. They may have even membered rings or be purely acyclic or may contain a mixture of rings and acyclic features (e.g., styrene, i.e., vinylbenzene or the benzyl system).

Even Alternant Hydrocarbon System: An alternant system which has an even number of carbon atoms in the conjugated system

Odd Alternant System: An alternant system which has an odd number of carbons.

Non-Alternant System: Contains an odd-membered ring in the conjugated system.

PROPERTIES OF THE MO’S OF ALTERNANT AND NON-ALTERNANT SYSTEMS

q All alternant hydrocarbon systems (but not non-alternant systems) have pi MO’s whose energies and coefficients are paired in terms of energy and coefficients:

o Paired means that for every BMO there exists an ABMO the energy of which is exactly as antibonding as the BMO is bonding. Also, the coefficients at each atom in the ABMO has the same absolute magnitude as the coefficient at that atom in the BMO, so that the electron distributions are the same.

q Odd alternant systems have, in addition to the paired BMO’s and ABMO’s, a single NBMO.

CYCLIC CONJUGATED SYSTEMS: Conjugated systems in which all of the carbons bearing 2p_z AO’s form a ring. Monocyclic means they are contained in a single ring.

PROPERTIES OF THE MO’S OF MONOCYCLIC CONJUGATED SYSTEMS

q Assuming that the ring has the shape of a regular polygon, the symmetry of the system gives rise to many orbital degeneracies (all MO’s except the lowest BMO, and in the case of an alternant system, its paired ABMO)..

q The lowest energy BMO is non-degenerate and highly bonding.

q Succeeding higher energy MO’s occur as doubly degenerate pairs.

q Alternant cyclic systems have paired MO’s.

q In non-alternant cyclic systems, there is of course no orbital pairing.

Resonance Energies. The lowering in energy of a conjugated system caused by the delocalization of the electrons over more than two atoms. This is the energy difference between the real, delocalized system and the energy it would be expected to have if were not delocalized (i.e., if it were fully localized). Typically, this is given as:

E_p -E_p^o = Energy of the actual pi system – Energy of the Hypothetical Localized Model

q The energy of the actual, delocalized pi system is given as:

E_p = S N_j E_j

q Where the summation is over all occupied orbitals (j). N_j is the orbital occupancy (number of electrons in that orbital) and E_j is the energy of that MO.

q The BMO of ethene has energy of a + b, and this MO has an occupancy of 2, so that the total energy of the pi bond of ethene is 2(a + b) or 2a + 2b.

q The energy of an electron localized in a 2p AO on carbon is the coulomb integral, a. Since a carbanion has 2 electrons localized on a single carbon, it has an electronic energy of 2a. A carbocation site has no electrons in the 2p AO, so it contributes nothing to the pi electron energy.

q The energy of the localized model (E_p^o) calculated as the sum of the energies of all the ethylenic pi bonds, carbocation centers, radical centers, and/or carbanion centers.

Charge Distributions

The charge density (Q_i) at a specific atom (i) is calculated as the difference between the electron density at that atom and the electron density that the atom should have when neutral (uncharged). In the pi electron approximation, that would be one, since a neutral carbon (as in the methyl radical) would have a singly occupied 2p_z AO.

Q_i = 1- S N_ja_ij² = 1- q_i

Where the summation is over all the occupied MO’s (j). and a_ij is the coefficient of atom i in a given MO (j).

q Alternant hydrocarbon systems (if they are not ions or ion radicals, i.e., they are overall electrically neutral) have zero charge densities at all carbons. Note that this is not true if there is a heteroatom in the sytem (atom other than carbon, such as oxygen or nitrogen). Thus, an etheneic double double is nonpolar, but a carbonyl double bond is highly polar.

q Non-alternant hydrocarbon systems can have non-zero charge densities at the various atoms.

Frontier Orbitals

The highest energy occupied MO is designated the HOMO, and the lowest energy vacant (unoccupied) MO is termed the LUMO. In a radical species, the orbital which contains the odd electron is termed the SOMO (singly occupied MO).

Spin Densities or Odd Electron Densities

Since the SOMO of a radical (or ion radical) species exclusively controls the distribution of the spin (the odd electron), the spin density or odd electron density (or radical character) can be calculated just from the SOMO coefficients. Square the coefficient of a given atom in the SOMO to obtain the spin density (r_i).

r_i = c_i,SOMO²

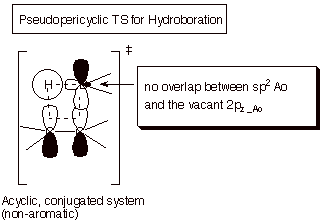
An addendum concerning mechanisms

You may recall that we have written the mechanism of the HCl addition to alkenes as a stepwise one, in which one bond is made first (the new C-H bond), followed by a second step in which the C-Cl bond is made. The question might well be asked, why doesn’t this reaction occur in the concerted manner of the hydroboration reaction? The answer is that the concerted addition of HCl would necessarily have a cyclic, conjugated transition state with four electrons, which would be antiaromatic. But then, why is the hydroboration reaction permitted to be concerted. The answer to this is especially interesting and informative. In the case of hydroboration, the Ts is not really cyclic (or pericyclic), because the sp² AO on boron (which is a part of the B-H bond) is orthogonal to (does not overlap at all with) the 2p_z AO on boron, which actually is the orbital which initiates bonding with the ethenic pi system. Such a reaction is called “pseudopericyclic” because it appears to have a cyclic system of orbitals, but this system is not completed. It is, in effect, an acyclic orbital system. Acyclic, conjugated systems are not sensitive to electron count.