CH 368: Unit 2
REACTION RATES, TRANSITION STATES, AND MECHANISMS
A. Transition State
Theory.
1. The Basic Equation.
According
to transition state theory, the rates of reactions are given by the following
equation:
![]()
where k is the rate constant
for a given reaction, k is Boltzmann’s constant, T is the absolute
temperature, h is Planck’s
constant, and DG* is the free energy difference between
the transition state and the reactants, i.e., the activation free energy.
The
value of (kT/h) is 6 x 1012 s-1.
According to transition state theory, the fastest reaction, i.e., one which has
no activation requirements, has a rate constant of 6 x 1012 s-1.
Keep in mind that rates of diffusion in various solvents are typically much
less than this, e.g., ca. 10-10 s-1, so that bimolecular
reactions in solution which have no activation requirements are diffusion
controlled, i.e., they occur at the diffusion rate of the solvent. The maximum
rate of transition state theory therefore is attained, insolution, only in
intramolecular reactions or quasi-intramolecular reactions (those in which two
molecules have initially formed a complex). Enzymic reactions can theoretically
also occur at this maximum rate.
The free energy of activation, like the standard free
energy change of a reaction, is composed of enthalpic and entropic parts, as
shown in the equation below, so that the basic equation of transition state can
be re-written in terms of these components.
![]()
2. Rate Constants.
The
rate constant, k, is independent of the concentrations of any reactants. It is
a measure of the intrinsic reaction rate, or the rate of the reaction at unit
molar concentrations of all reactants. The overall rate is equal to the rate of
consumption of reactants or the rate of formation of products (usually equal).
Clearly the rate of product formation in a simple intramolecular reaction is
proportional to the concentration of the reactant. The rate constant, however,
is independent of the concentration, and this rate constant is what is
predicted by transition state theory.

3. Definition of
Transition State.
The
transition state of a reaction step is considered to be the highest energy
point on the minimum (free) energy reaction path (MERP). Reactions are
considered to occur via the path
from reactants to products which is of lowest energy. The TS is the point of
highest energy on this path. As such it represents a saddle point on the free energy surface. On the free energy
multidimensional surface, it is an energy minimum with respect to every other variable
except the reaction path.
4. Reaction Coordinate.
The reaction coordinate, in a purely qualitative
sense, represents the extent to which the coordinates (values of various bond
lengths, angles, and dihedral angles) which characterize the reactants have
been converted to those of the products as progress is made along the MERP.
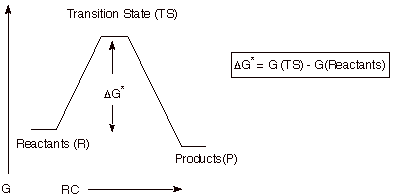
5. Reaction Path Diagrams.
Reaction path diagrams, as represented above, are a
two dimensional slice of a multidimensional energy surface for the reaction.
Conventionally, they are a plot of energy (in the rigorous case, free energy,
G) versus the reaction coordinate.
6. Reaction Mechanism.
The mechanism of a reaction is a stepwise
description of how reactants are converted to products. Of course, some reactions occur in a single step, as
represented in the reaction path diagram above. Such reactions are termed concerted. More generally, reactions are found to occur in a
stepwise fashion. They may consist of 2,3 or many more steps. In any stepwise
reaction, intermediates (I) must be formed. By definition an intermediate is
any species encountered on the reaction path between R and P which represents a free energy minimum. As simple illustrations of stepwise
mechanisms, we will consider two distinct scenarios for reactions which occur
in two steps.
- First Step Rate-Determining.
Mechanism:
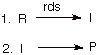
Reaction
Path Diagram:
The
term “rate-determining step” or “rds” has a specific
meaning. An rds is a step of a reaction the rate of which is equal to the rate
of the overall reaction (conversion to final product(s)). The importance of a
rate-determining step is that if the rate of that step is known, the rate of
the overall reaction is known. To put it another way, we do not need to know
the rates of any of the other steps of a multi-step reaction if we know the
rate of the rds. The conditions for a rate-determining step are, however, quite
restrictive. As noted in the scheme above, the intermediate must always go on
to product (never back to reactant; so a reversible step can not be
rate-determining). To the extent the intermediate reverses to reactants, the
rate of final product formation is less than the rate of forming the
intermediate. This restriction means that the activation energy for the reverse
of the first step must be substantially greater than the activation energy for
the second step. Secondly, the intermediate must not build up in concentration,
but must go on to product very rapidly. This means that the barrier to the
second step must be very small.
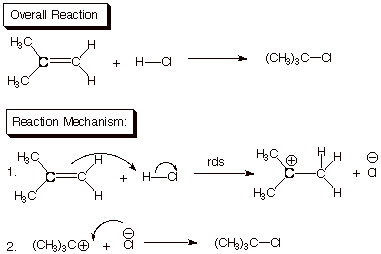
Exemplification. The addition of hydrogen chloride to an alkene such
as isobutene is a typical example of a two-step reaction in which the first
step is rate-determining. Note that the overall reaction requires breaking two
bonds (the C=C pi bond and the H-Cl bond) and forming two bonds (the C-H bond
and the C-Cl bond). However, these four primary bond changes do not occur
simultaneously in a concerted reaction; this pathway is of much higher energy
(we will see why later), and is not the minimum energy reaction path. In the
minimum energy path, two bonds are broken in the first step and only one is
formed. Therefore, the intermediate carbocation/chloride ion pair is at a much
higher energy than the starting materials. Consequently, the activation free
energy for this step is rather large (it has to be at least as large as the energy difference
between the intermediate and the reactants). The intermediate, once formed, has
a very low barrier to going on to the product, since no bonds are broken in
this second step, while one new bond is formed. The intermediate essentially
always goes on to product because the barrier toward the reverse of step 1, in
which the chloride ion would remove a proton from the intermediate carbocation
to yield back the reactant alkene and hydrogen chloride, is substantially
larger than the very small barrier to step two. Therefore, both conditions for
a rate-determining step are fulfilled, viz., the intermediate always goes on to
product, and it doesn’t build up in significant amounts.
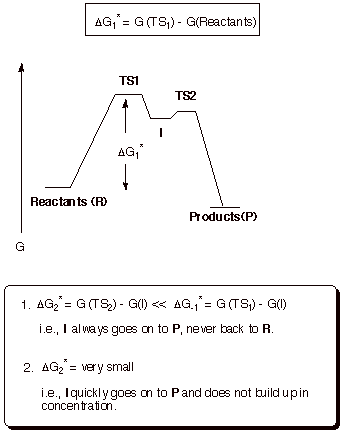
b. Second Step Rate-Determining.
Reaction Path Diagram
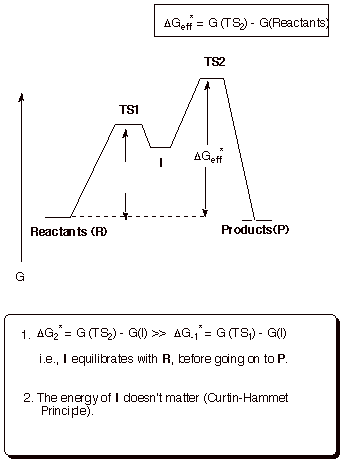
In
this mechanistic scenario, the intermediate is formed in a reversible
equilibrium, and then slowly goes on to the products. The effective barrier for
the reaction is the energy difference between the second TS and the original
reactants. Neither the energy of the 1st TS not the energy of the
intermediate is of immediate consequence in this scenario. The intermediate may
be formed in detectable amounts or it may be formed in minute amounts. Either
way, the energy of the intermediate is irrelevant to the rate of the reaction .
This principle is called the Curtin-Hammett principle. If the intermediate is
of relatively low energy, it will be formed more extensively, but the
activation energy for promoting it to the second TS will then be
correspondingly higher.
B. Transition State
Models.
1. Resonance Theoretical
Approach.
a. A Polar Transition
State. For relatively simple reaction systems, transition
states and their energies (therefore activation energies) can be calculated.
For qualitative purposes, resonance theory provides a very convenient approach
to transition state modeling. The basic principles involved are as follows:
q
Transition states are
generally intermediate between reactant and product in their geometry and, for
the most part, in electron distribution. Consequently, the TS should be
reasonably represented as a resonance hybride of reactant and product-like
structures (at the unique geometry of the TS).
q
In some cases, since the
TS is a unique entity, and since resonance theory indicates that a given
species is best represented as a resonance hybrid of all reasonably good
resonance structures, one or more non-reactant and non-product-like structures
may be a further improvement.
q
Since the real TS is
intermediate between the canonical structures, some of the bonds will be
partial, because a given bond is made in some structures and broken in others.
These partial bonds can be represented as dashed lines in a dashed line/partial
charge structure. In the same way, charges on some atoms will be intermediate
between unit charge and zero charge, and these can be represented as partial
charges using the d formalism.
q
The DL/PC model can then
be examined and characterized by means of the salient characteristics of the
model. Subsequently, the Hammond Principle can be applied to refine the TS
character(s).
Consider,
as an example, the addition of HCl to ethene.
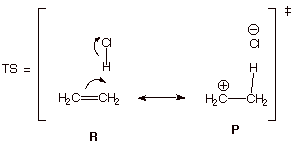
The structures of ethene and HCl, as reactants, are
oriented in the proper manner to qualitatively represent the anticipated TS,
i.e., protonation of one of the carbons of ethene. Then use the electron flow
formalism to generate the product structure, i.e., the ethyl carbocation and
chloride anion, still in the same orientation.
Following
this, summarize the model as a single DL/PC structure, using dashed lines for
partial bonds and Greek delta’s for partial charges.
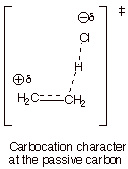
q
Since the C-C bond is
double in the reactant structure and single in the product structure, it must
be intermediate between single an d double in the TS. This is represented as a
full line for the sigma bond and a dashed line for the partial pi bond.
Simliarly, the new C-H bond is made in the product but unformed in the
reactant, so it is also intermediate between no bond and a single bond. Again,
a dashed line represents this partial bond, as it does also in the case of the
H-Cl bond, which is full (bond order of 1.0) in the reactant and broken (bond
order of 0) in the product.
q
In a similar way, unit
positive charge appears on the passive carbon (the one not bonding to the
proton) in the product, but there is no charge on that carbon in the reactant.
Consequently, this is represented as a partial positive charge on the passive
carbon. When we apply the Hammond Principle, we will be able to be more
specific about how much charge is present there. Correspondingly, there isi
partial negative charge on the chlorine.
q
Finally, the formal
characterization is presented, i.e., carbocation character at the passive
carbon.
b.Radical Transition
States.
In
the same way, radical addition, abstraction, or other transition states can be
modeled using resonance theory. For example, the abstraction of hydrogen atoms
from an alkane by bromine atoms:
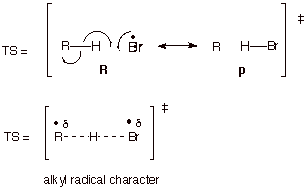
c. Inclusion of Non-R
non-P Structures.
Resonance theory indicates that the best
representation of a structure is a combination of all canonical forms of
reasonable energy. Although essentially any TS should have R and P character,
the TS may have additional characters not present in either the reactant or
product, though these additional structures, which we will term X structures.
We will consider two important examples of this type.
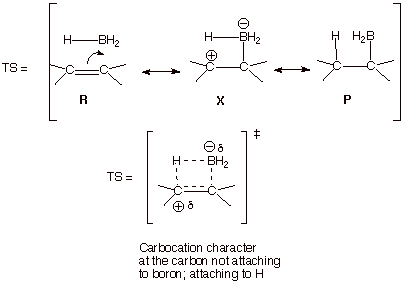
i. Hydroboration. The addition of borane to an alkene has been shown to
be influenced, in its regiochemistry, by polar effects which uniquely exist in
the transition state. Besides the reactant and product-like structures, an
additional polar structure can be written which recognizes the Lewis acidity or
electrophilicity of trivalent boron. As a consequence, there is carbocation
character at the carbon to which the hydrogen becomes attached.
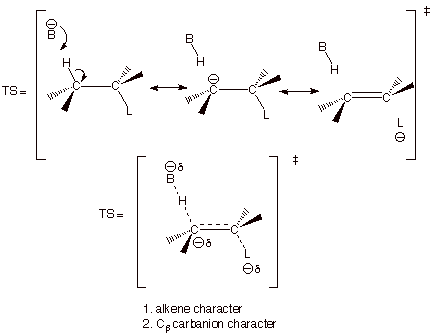
ii. E2 Eliminations. Although E2 eliminations are typically discussed in
terms of predominant alkene (P-like) character in the TS, there is another
significant character in that TS which, in some cases, becomes the dominant
character. As a result of the carbanion character at the beta carbon, certain
eliminations prefer to yield the less thermodynamically stable alkene.
2. The Hammond Principle. The treatment of transition states as resonance
hybrids of reactant-like and product-like structures (along with any other
“good” structures) implicitly takes into account the circumstance
that virtually any transition state has some reactant-like and some product-like
character. The treatment does not, in itself, indicate how much of each one or even whether the TS more closely
resembles one or the other or is very centrally located between the two. The
Hammond Principle is extremely useful in refining transition state models in
the sense of knowing whether the TS strongly resembles reactants or products or
is rather centrally located between them. In its most succinct form, the
Hammond Principle states that “The transition state of an
elementary reaction step more
closely resembles the reaction partner (i.e., reactant or product of that step)
which is of higher energy.”
Consequently the TS of a reaction step which is endothermic more closely
resembles the product of the step, and a the TS of a reaction step which is
exothermic more closely resembles the reactant. As a corollary of the Principle, reaction steps which are
highly endothermic, have TS’s which closely resemble the product of that
step, and reaction steps which are highly exothermic have TS’s which
closely resemble the reactant in that step. Reaction steps which are neither
strongly endothermic nor exothermic, but roughly thermoneutral are considered
to have centrally located transition states.
As
an example of a highly endothermic step we can consider the protonation of an
alkene by hydrogen chloride. In this reaction step, two bonds are broken (the
H-Cl bond and the C-C pi bond), and only one new bond is formed (the C-H bond).
Consequently, the formation of the carbocation intermediate in this step is
highly endothermic, and the TS for this step closely resembles the product of
the step, which is a carbocation. We can then refine our characterization of
the TS model to say that the TS has “extensive carbocation character
at the passive carbon.” Experimental evidence indicates that
the TS has indeed developed between 80-90% of the unit positive charge present
in the full-fledged carbocation intermediate. The special importance of this
refinement in our characterization lies in the implication that it has for selectivity.
If there were only a small fractional positive charge developed on the passive
carbon in the TS, the distinction between
TS’s which have primary, secondary, or tertiary carbocation
character would not be quantitatively very great, so that selectivities (e.g.,
regioselectivity) and relative rates of addition of HCl to various alkenes
would be quite small. Selectivity is, of course, a matter of prime importance
in the utilization of organic reactions.
As
an example of a highly exothermic reaction, we can consider the second step in
the reaction of HCl with an alkene, i.e., the reaction of the intermediate
carbocation with chloride ion. In this step, no bonds are broken, and one is
formed, so that the reaction is highly exothermic. In this case, the Hammond
Principle indicates that the TS resembles the reactant of the step, which is
(again) the carbocation. Interestingly, the TS’s of both reaction steps
strongly resemble the carbocation intermediate.
As
examples of reactions which are neither highly exothermic nor highly
endothermic, we can consider either the hydroboration of an alkene or the
elimination of HCl in an E2 reaction, both of which have been previously
discussed. Note that in both cases, the mechanism is a concerted one. In both cases,
also, two bonds are broken and two are formed, so that neither reaction is
highly exo- or endothermic. The
reaction, since it goes to completion, must be exergonic (and it is also
exothermic), but it is not a highly exothermic process. Consequently, the TS
does not strongly resemble either the reactants or products, but is centrally
located.
3. The Method of Competing
Transition States. Chemistry, like much else, is a competitive world.
Competition determines the outcome of chemical reactions, i.e., whether a given
reaction is successful in generating a desired product in good yield, or this
product is obtained as a mixture or in very low yield. In general, the outcome
of any competition is determined by therelative activation free energies of each
competing mechanism. If the reactants are the same for each of the competing
processes, the situation simplifies further: the results of the competition
are determined by the relative free energies of the transition states of each
mechanism. It is transition states which actually compete!! At room temperature, for example, for each 1.37
kcal/mol of difference in the free energies of the TS’s, a ten-fold rate
ratio results. This would provide
an approximately 91:9 ratio of the products. If one desires higher selectivity,
e.g., 99:1, a 2(1.37) = 2.74 kcal/mol energy difference would be required.
A. Regioselectivity (or
Regiospecificity). The reaction of
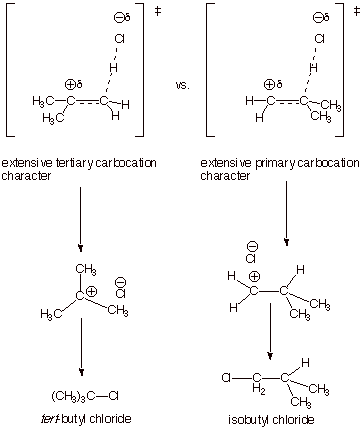
an unsymmetrically substituted alkene, such as isobutene, with an unsymmetrical
reagent such as hydrogen chloride could potentially generate either or both of
two products, i.e., tert-butyl chloride or isobutyl chloride. These are
products which results from combining the two unsymmetrical reactants in the
two different orientations. Orientational selectivity such as this is often
referred to as regioselectivity. In reality, one of these products (tert-butyl
chloride) is obtained with a very high level of selectivity, i.e., essentially
none of the other product (isobutyl chloride) is obtained. Nevertheless, the
results of the reaction of isobutene with hydrogen chloride are determined by
the outcome of a competition (it turns out not a very close competition)
between two distinct reaction mechanisms and, in particular, two distinct
transition states. To understand the strong preference for formation of
tert-butyl chloride over isobutyl chloride we need to create TS models for both
TS’s and compare their refined and extended characters. To do this, we
have only to utilize our previously derived TS model for the addition of HCl to
ethene and convert the hydrogens
of the ethene TS to the desired substitutents, as shown in the scheme below.
The difference between the two TS’s is easily evident. One has tertiary
carbocation character, and the other has primary carbocation character. Since
tertiary carbocation character is more favorable than primary carbocation
character, the TS on the left is favored, and the preferred product is tert-butyl chloride. The high selectivity is rationalized
by two considerations: (1) a full-fledged tertiary carbocation in solution is
more stable than a primary one by at least 30 kcal/mol, a very large preference
(2) the TS’s both have extensive carbocation character (via the Hammond
Principle), so that a very large fraction of the total energy difference
between a tertiary carbocation intermediate and a primary carbocation
intermediate is incorporated into the TS. Consequently, the TS on the left is
powerfully favored, and the selectivity is extremely high.
B. Relative Rates. When comparing the relative rates of reaction of different molecules, e.g., the relative rates of addition of HCl to a series of different alkenes, differences in the free energies of activation of the competing reactions could arise from either transition state energy differences or differences in energy of the different reactants. In the case of HCl addition to alkenes, the energy differences between simple alkenes are quite small compared to TS energy differences, which are based upon differential carbocation character. Consequently, the Method of Competing TS’s is still a very appropriate approach to use in discussing the relative rates of addition to alkenes.
Consider
the following series of simple alkenes: ethene, propene, isobutene, and trans-2-butene. Again using the basic TS model for the
rate-determing step of these reactions, we can perform the requisite
substitution of alkyl groups for the four hydrogens of ethene or for the four
unspecified bonds of a general alkene and set up a TS for each of these
alkenes.
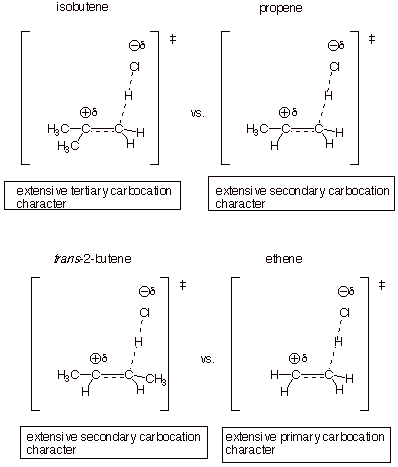
In the case of
unsymmetrically substituted alkenes (propene and isobutene), we will ignore the
disfavored regioisomeric TS. We can then characterize these TS’s and rank
them according to their expected relative energies. We can also apply the
Hammond Principle to gain insights into the expected magnitudes of the relative
rate differences. We note that isobutene has thebest TS, since it has extensive
tertiary carbocation character, while propene has extensive secondary
carbocation character, and ethene has extensive primary carbocation character. Trans-2-butene is especially interesting because, although
it is a disubstituted alkene, like isobutene, its TS has only secondary
carbocation character, like that of propene. This is because the carbocation
character is generated on only one carbon atom of the original alkene double
bond, specifically the passive carbon, so that the second methyl group of
2-butene is not attached to a carbocation center and does not have a major
effect upon the rate. Consequently, the rate of addition to this alkene is
similar to that of propene.
The
relative rate ratios will be large (i.e., isobutene reacts very much faster
than propene, e.g.), because there is extensive carbocation character, and the
energy difference between tertiary carbocations and secondary carbocations is
very large. In contrast, relative rate ratios for hydroboration are rather
small, because the TS has only a modest amount of carbocation character.