Unit 4: Free Energy Relationships

The Hammett Equation.

The correlation of reaction equilibria and rates with changes in structure is a major goal of chemistry. In organic chemistry, the change in an equilibrium constant, K, or a rate constant, k, which results from the substitution of a specific group for hydrogen, the so-called substituent effect, is of special interest. Professor L.P. Hammett, of Columbia University, systematized much of the research in this area by defining a quantity s (the substituent constant) for any given substituent.as follows:

where K_ois the acid dissociation constant for the ionization of benzoic acid and K is the acid dissociation constant for the ionization of a substituted benzoic acid with a given substituent at a given position on the aromatic ring. Since log K_o is directly related to the standard free energy change accompanying the ionization of benzoic acid (via DG^o = -2.303RTlog K_o ), and log K is directly related to the standard free energy change accompanying the ionization of the substituted benzoic acid, the substituent constant is actually related to DDG^o, the difference in the free energy changes for the two ionization processes, i.e., a measure of the substituent effect expressed in terms of a free energy quantity. Since the K’s depend somewhat upon the temperature and critically upon the nature of the solvent, s is defined specifically for water at 25 ^oC. Also, since the magnitude of the substituent effect depends upon the position of the subsituent upon the aromatic ring, there are different substituent constants for para, meta, and ortho substituents. Typically, these are distinguished as s_p , s_m , and s_o . 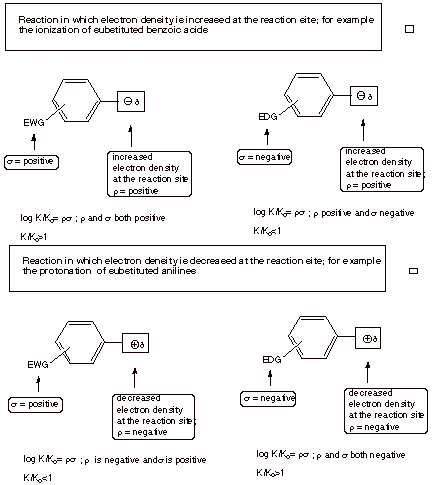If the ratio (K/ K_o) >1, i.e., the substituent has increased the acidity of the benzoic acid, s is positive. Such a substituent is considered to be an electron-withdrawing group (EWG), because electron density is increased at the reaction site in the product benzoate anion, and an EWG will favor this change by withdrawing electron density away away from the reaction site. Groups such as m-Cl, p-Cl, m-NO₂, p-NO₂, etc. which have relatively large dipole moments oriented with the positive end directed toward the reaction site are EWG’s. On the other hand, electron donating groups (groups which tend to increase the electron density near the reaction site) disfavor the ionization to a negatively charged ion and have K/K_o<1. These groups have negative sigma values. These include alkyl groups (at both the meta and para positions), para alkoxy groups, and p-amino groups. The Hammett substituent constants for many hundreds of substituent groups have been measured and tabulated. It should be noted that, by definition, Hammett substituent constants are relative to hydrogen as a basis of comparison.That is to say, s_H = 0.0.

HAMMET SUBSTITUENT CONSTANTS

Hammett sconstants are based upon the acid dissociation of benzoic acid and m- and p-substituted benzoic acids in water at 25 ^oC. The K_a’s of some of these acids are given in the table below:

Substituent (X)	K_a	pK_a	s_p	EWG or EDG
p-OCH₃	3.5x10^-5	4.46	-0.27	EDG
p-CH₃	4.3x10^-5	4.34	-0.17	EDG
H	6.46x10^-5	4.19	0.00	Standard
p-Cl	1.10x10^-4	3.96	0.23	EWG
p-NO₂	3.90x10^-4	3.41	0.78	EWG

The sigma values are derived from the equation below:

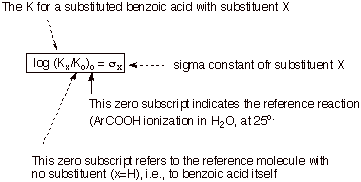
Note that is X=H, the sigma value is exactly zero, by definition. Also note that EDG’s have negative values of sigma because these substituents cause a decrease in the ionization constant (we will see why). EWG’s have positive values of sigma, because they cause an increase in the ionization constant relative to that of parent benzoic acid. These constants not only give us an idea of whether a given substituent is electron-withdrawing or electron-donating relative to hydrogen, but they also give us a qualitative and quantitative sequence of EWG-power or EDG-power. Please not, as we will see, that a para X has a different sigma value that a meta X. That is why in our first table we specified the para positioning of the substituents. Ortho substituents are not usually treated within the context of the Hammett equation because steric effects can interfere with the purely electronic effects, and these steric effects are highly variable from reaction to reaction.

The Hammett Equation (given below) then asserts that these same substituents will have effects upon the equilibrium or rate constants for any other reaction which linearly parallel those in the benzoic acid ionization. The proportionality constant (i.e., the slope of the line) r, will vary with the particular reaction under study, but its magnitude reveals the degree of sensitivity the reaction has to substituent effects. If it is greater than 1, it is more sensitive to substituent effects than the standard benzoic acid ionization. Here is is appropriate to note that the rho value for benzoic acid ionization is, by definition, exactly 1.000. If the rho value for a given reaction or equilibrium is less than 1, it is less sensitive. On the other hand, if it is negative, it indicates that substituents affect the reaction in the opposite way from the standard reaction, i.e., EWG’s slow the reaction rate or suppress the equilibrium and EDG’s accelerate the rate or favor the equilibrium. Since the benzoic acid ionization generates a negatively charged product, and this corresponds to a positive rho value (by definition), a negative rho corresponds to the development of position charge (or the quenching of negative charge).

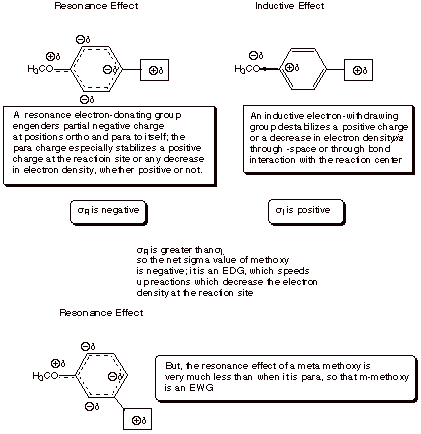
Para vs Meta Subsituents: Resonance and Inductive Effects. Substituents exert the electronic effects expressed in Hammett correlations via two main types of effect, resonance and inductive effects. To illustrate the resonance effect, consider the p-methoxy substituent. Because of a resonance interaction between a filled 2p AO on the directly attached oxygen and the pi system of the ring (via the ipso carbon), the methoxy substituent places a substantial amount of excess electron density (negative charge) upon the ring. However, this charge is selectively placed upon the ortho and para positions of the ring, as opposed to the meta position. Consequently, of the methoxy group is para to the reaction center, it generates negative charge upon the ring carbon directly attached to the reaction center’ attachment. This is the main effect of the p-methoxy group, which makes it a rather strongly EDG. By the way, a small effect of this resonance is felt even when the methoxy is meta to the reaction center, because of the negative charge generated at positions ortho to the reaction center. Since these centers of negative charge are further away from the reaction site, the effect is much smaller, and the m-methoxy group is actually EWG. This is the result of its electron withdrawing inductive effect. The para substituent constant is considered to be a sum of the resonance sigma value and the inductive sigma value, while the meta sigma value is the sum of the inductive sigma and a fraction of the resonance sigma.

As an example, the meta sigma value of chlorine is 0.37, while the para sigma is only 0.22, i.e., both substituents are EWG, but the meta one is more strongly so. Note that the inductive effect is dominant for the halogens., in part because they are poorer electron donors via the resonance effect than is oxygen. Also, the meta sigma of methoxy is +0.11 (it is EWG), while the para sigma is –0.27 (it is EDG). Strong evidence exists that the inductive effects in the meta and para positions are very similar. So for para methoxy, the resonance effect is dominant over the inductive effect, but both are significant. For an amino group, the electron donating power is even greater. Note also that the sigma for p-SCH₃ (0.00) is less negative than that for p-methoxy, even though the inductive effect of sulfur is surely less than that of oxygen. This is apparently because of an orbital mismatch; that is, the larger 3p AO of sulfur overlaps less efficiently with the smaller 2p AO of the attached ring carbon, resulting in a much smaller resonance effect in the case of sulfur substituents. For the same reason, a p-fluoro subsituent (+0.06) is less strongly electron withdrawing than a p-Cl )+0.23) or Br substituent.

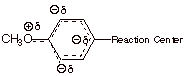
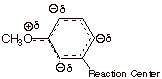
Hammett further observed that if log (K/ K_o) for the ionization of other acids was plotted versus these sigma values, reasonably linear plots were obtained. For example, if the log (K/ K_o) data for the ionization of meta and para substituted phenylacetic acids in water at 25 ^oC was plotted versus his sigma values a linear plot of slope 0.489 was obtained. Similarly, if the data for ionization of substituted phenylpropionic acids was plotted vs sigma, a linear plot of slope 0.212 was obtained.

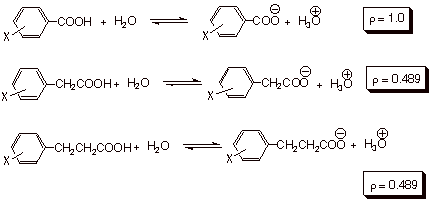
Hammett therefore proposed the equation now known by his name:

where log (K/ K_o) represent the log of the relative equilibrium constants for any reaction, with the K for the substituted reactant in the numerator and the K_o for the unsubstituted version in the denominator. The value of the proportionality constant, rho, depends upon the specific reaction being studied, and was termed the reaction constant. Essentially, the Hammett equation proposes that the relative free energy changes occasioned by the changes in substituent are proportional the same changes in the benzoic acid series, or for that matter to any other series of equilibria. The magnitude of rho, in effect, determines how large the free energy changes are in a reaction series, that is, how large the substituent effects are. If K>1, the substituent effects are larger than in the standard benzoic acid ionization. If K<1, the substituent effects are smaller than in the standard reaction. We can easily see that the substituent effects are smaller for the arylpropionic acid series than for the arylacetic acid series, than for the standard reaction. Essentially this is because the change in electron density occasioned by the loss of a proton for the carboxyl group, although the same in each of these reaction series, is closest to the substituent and the aryl ring in the standard series and most remote in the arylpropionic acid series. The substituent effect is thus least in the latter series because of the remoteness of the reaction site from the substituent and the aryl ring.

In the ionization of phenols, the negative charge is generated at a benzylic-type position, i.e., it is generated on an atom (oxygen) which is directly attached to the ring. The rho value for the ionization of substituted phenols in water at 25 ^oC is, correspondingly greater than that for the standard benzoic acid ionization (2.1)

When the reaction site is actually in the aromatic ring, the substituent effects, as reflected by the rho value, are even larger than in the standard reaction series. This is seen in the ionization of substituted pyridinium ions in water at 25 ^oC, where r = +5.2. Incidentally, the second equation below indicates that the rho value for the reverse of a reaction has the opposite sign, but the same magnitude as for the forward reaction. In general reactions, like the standard reaction, in which electron density is increase at the reaction site, have positive rho values (posite rho may be taken as a positive increase in electron density). Reactions in which the electron density at the reaction center is decreased in going from reactant to product have negative rho values. The seoncd equation below is an example of the latter kind, in which a positive charge is generated at the reaction site. From the first equation below we should note that electron density increases do not require the development of a negative charge. The removal of a positive charge is equally as good at increasing electron density.

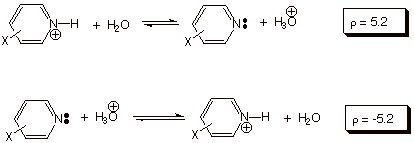
We have seen that rho values depend quantitatively upon the distance of the electron density change from the aryl ring. They also depend, of course, upon the magnitude of the electron density change. The development of partial negative charges is best seen in a context of the correlation of reaction rates with substituent constants (see below). However, a similar effect can be seen in the dependence of the magnitude of rho, for a given reaction, upon the nature of the solvent. As we have seen, the rho value (by definition) for the standard reaction series (in water) is 1.0. If the solvent is changed to methanol, the rho value increases by about 50%, to 1.54. In solvent ethanol it increases to almost twice the value in water (1.96). In acetonitrile, a further increase to 2.8 is observed. Clearly, solvation has a major effect on the magnitude of substituent effects, being largest when the carboxylate ion is not as highly solvated by hydrogen bonding. In effect, hydrogen bonding to the carboxylate ion partially quenches the unit negative charge on the carboxylate anion. Consequently, the rho value is least in water, the best hydrogen bonding solvent of all.

Correlation of Reaction Rates with Hammett s Values. In an entirely similar way, relative rate constants for various reaction series can be correlated with substituent constants. In this case, of course, the free energy changes referred to are between reactant and transition state. Once again, if electron density is increased in the TS relative to the reactant, positive rho values are expected, i.e., electron withdrawing groups will accelerate the reaction. If electron density is decreased, EDG’s will speed the reaction. The Hammet equation as applied to relative reaction rates would be expressed as follows:

where, as before, k is the rate constant for the substituted version of the reactant and k_o is the rate constant for the unsubstituted version of the reactant (X = H). As before, larger rho values can correspond to electron density changes which are closer to the aryl ring, but in the case of transition states, also to larger changes in electron density. This is because transition states can have partial charges.

The Substituent Constants. It is generally understood that substitutents exert their effects by means of two distinct electronic mechanisms, resonance effects and inductive effects. The latter are essentially electrostatic attractions or repulsions resulting from the dipole moment of the ring C-X bond and its differential interactions, both through space and through bonds, with the reaction centers in the reactant and in the product or transition state. Resonance effects are exerted through the increase or decrease in pi electron density in the aromatic ring as a result of pi overlap between the 2p AO on the directly attached ring carbon and an orbital (usually a p AO) on the substituent. Both inductive and resonance effects are somewhat position specific, but inductive effects tend to be quite similar for the same group when situated in either the meta or para position. In sharp contrast, resonance effects are very small for meta substituents, since partial charges induced by resonance are specific to the positions ortho and para to the substituent. Therefore resonance effects are especially large for para substituents. The following equations express these relationships:

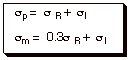
As a rough approximation, the resonance sigma parameters can be obtained by just subtracting the meta sigma values from the para sigma values.

Hammett Substituent Constants

Substituent	s_p	s_m	s_p - s_m (ca. s_R)
NMe₂	-0.83	-0.21	-0.62
OMe	-0.27	+0.12	-0.39
CH₃	-0.17	-0.07	-0.10
H	0.00	0.00	0.00
F	+0.06	+0.34	-0.28
Cl	+0.23	+0.37	-0.14
CO₂Et	+0.45	+0.37	+0.08
CH₃C=O	+0.50	+0.38	+0.12
NO₂	+0.78	+0.71	+0.07
NMe₃+	+0.82	+0.88	+0.06

where the resonance contribution to the overall sigma constant is represented as s_R and the inductive contribution as s_I. Groups which are electron donating in a resonance sense are of two sub-types: (1) those, such as –Cl, -OR, SR, and NR₂ which have an unshared electron pair on the atom attached to the ring, which can donate electrons to the ring via resonance (2) alkyl groups, which can donate electrons via hyperconjugative resonance. These groups, being electron donors, therefore have negative values of s_R. Those substituents in the first group have positive values of s_I, since their sigma bond dipoles are oriented with the positive end nearest the ring. There is therefore a tendency of these two effects to operate in opposite directions. For nitrogen and oxygen groups, where resonance effects are the strongest, the resonance effect is dominant over the inductive effect, and the net sigma value negative (EDG’s). The electrons on nitrogen in the amino functions, such as amino or dimethylamino, are less tightly held than those on oxygen in the oxygenated substituents such as hydroxy or methoxy, so the resonance effect is larger for oxygen-center substituents. Also, the sigma bond dipole, and therefore the inductive effect, is diminished in the case of nitrogen as compared to oxygen. Since resonance effects are larger and inductive effects are smaller for nitrogen, the amino substituents are more strongly electron-donating than the alkoxy substituents. It may be interesting to think about why the sulfur substituents are less strongly donating that the corresponding oxygen substituents (there is an orbital size mismatch between the 3p orbital on S and the 2p orbital on carbon, leading to less efficient overlap).

Hammett-Brown s⁺ Constants. In the case of reactions in which positive charge is generated on a benzylic carbon (as in an S_N1 reaction of certain benzylic halides or tosylates) or directly upon the aromatic ring (as in electrophilic aromatic substitution), the resonance effects of substitutents are rather strongly enhanced. In such cases, such that standard Hammett sigma parameters are longer valid. In particular, the rates of reaction of substrates having para electron donor groups such as methoxy, methylthio, dimethylamino, and even alkyl groups are much faster than would be predicted by the Hammett sigma values. Even para halogen substituents , which are resonance electron donor substituents, are much less rate retarding than would be expected from Hammett sigma values. Amazingly, para fluoro substitutents can even be modestly rate enhancing. These enhanced resonance effects apparently arise as a consequence of the direct resonance interaction of the positively charged reaction site with the para group via quionoidal resonance forms such as those shown below. Since these interactions are impossible when the substituent is

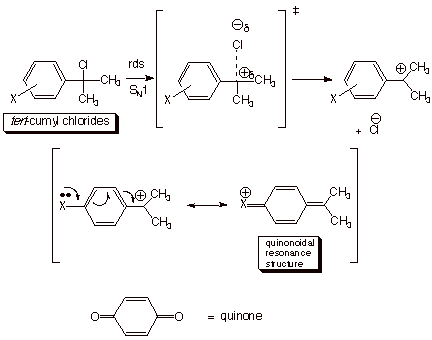
attached to the meta position, and are not operative for even a para resonance-electron withdrawing substituent like nitro or acetyl, the sigma values of these latter kinds of substituents are still valid. By plotting the data for the solvolysis of tert-cumyl chlorides and establishing the regression line on the basis of the meta substituents and the para resonance-EWG substituents, H.C. Brown derived a new set of sigma constants for the para resonance-EDG substituents, and designated them as s⁺ values.

Para Substituent	s Value	s⁺ Value
-NMe₂	-0.83	-1.7
-OCH₃	-0.27	-0.78
-SMe	0.00	-0.60
-CH₃	-0.17	-0.31
-Cl	+0.23	+0.11
-F	+0.34	-0.07

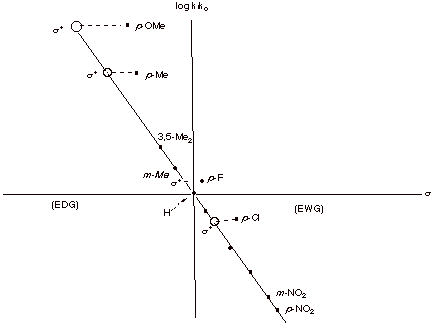
These same values are useful for the correlation of data for electrophilic aromatic substitution, where analogous quinonoidal resonance interactions are feasible.

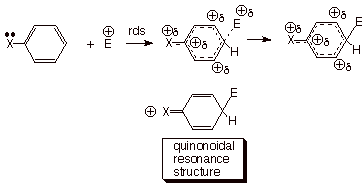
Rho Values for Various Electrophilic Substitutions. The rate-determining step for most electrophilic substitutions is the attack step in which the electrophile reacts with the aromatic to form the arenium ion. The degree to which the TS for this reaction resembles the arenium ion is a major determinant of the size of the rho value for a particular type of electrophilic substitution. For bromination, the rho value is quite large (-12.1), indicating a TS which strongly resembles the arenium ion. This is consistent with the accepted mechanism, in which neutral bromine is the (relatively mild) electrophile, so that the attack step is strongly endothermic. In Friedel-Crafts acylation, where the active electrophile is the acylium cation, the rho value decreases to-9.1. The rho value for nitration in acetonitrile is –6.2.

s ^- Values. Analogous enhanced resonance effects are encountered for para resonance-electron-withdrawing substituents when negative charge is generated on a benzylic atom (as in the ionization of phenols to phenoxide ions) or upon the aromatic ring (as in nucleophilic aromatic substitution). These same substituent constants, called s ^-_,are also applicable to the ionization of anilinium ions to substituted anilines, where a negative charge is not developed, but the strongly resonance electron donating amino group of the product interacts via the typical quinonoidal resonance interaction with resonance EWG’s present at the para position.

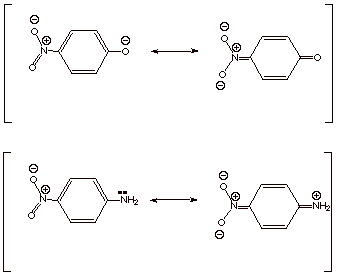
A typical Hammet plot for the dissociation of phenols is shown below. The regression line is defined by all of the resonance-electron-donating groups and by meta groups whether they are EDG or EWG. Only the para resonance-EWG groups such as nitro, cyano, and carbethoxy deviate, and their deviations are quite large. Whereas the sigma value for p-nitro is 0.78, the s^- value is 1.27! On the other hand, the sigma value for meta nitro does not require any change, i.e., the s^- value is the same as the s value.

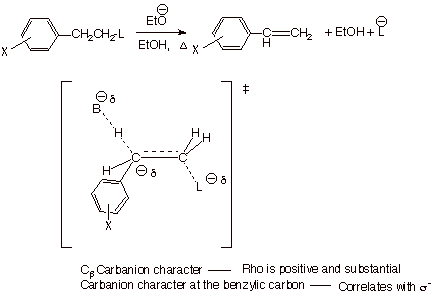
Detecting the C_b Carbanion Character in E2 Eliminations. We have previously developed a TS model for E2 eliminations in which the TS has both alkene character and C_b carbanion character. Through the study of the rates of E2 elimination of a series of m- and p-substituted b-phenylethyl chlorides and the correlation of the rates with the Hammett-Brown s⁺ constants, the projection that carbanion character is developed on the beta carbon can be experimentally affirmed. The observed rho value is +2.61. When the leaving group ability is diminished by using fluorine as the leaving group, the rho value increases to +3.12, indicating that carbanion character is now even greater at the beta carbon. Finally, when the leaving group is trimethylammonium ion (remember the Hoffmann elimination?), the carbanion character increases further to +3.8. This can explain why Hoffmann-type eliminations do not give the more stable alkene as the predominant product, but correspond to generating the TS which has the more stable carbanion character (primary>secondary>tertiary).