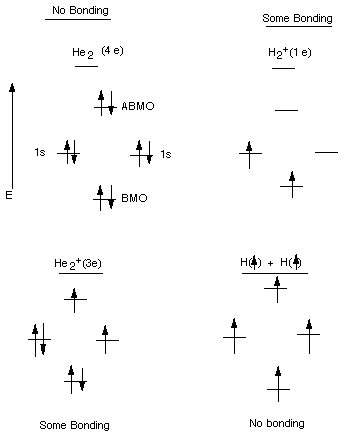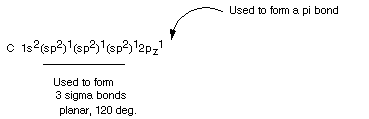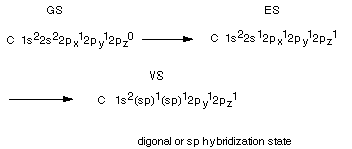Ch 610a, 618a: Fall Semester,
2003
Professor Nathan L.
Bauld
Beginning
TABLE OF CONTENTS FOR THIS
PAGE
LECTURE #1
Philosophy
- PERSONAL TEACHING EMPHASES (IN ORDER OF PRIORITY): (1)Reaction
Mechanisms--Understanding how reactions occur at the molecular level
(2)Theory--Understanding why reactions occur in the way they do (3)
Synthesis--Understanding how to use reactions to convert one compound
into another.
- GOALS: (1) Develop rigorous, systematic reasoning processes
valid in chemistry and related sciences (2) Develop understanding of chemistry
(3) See the beauty and utility of chemistry as the "central science".
- SPECIAL URGENT ADVICE:
This course very strongly emphasizes the lecture material and therefore has
as its standard the mastery of this material to a very high level of excellence
and detail.
- STUDY AIDS: (1)Emphasis Topics
for each chapter are available on these web pages.(2)Answer
Keys for Last Year's Exams are also included in these web pages(3)The
Instructor's Notes are also on these web pages(4) Problems in the textbook--as
assigned in your syllabus (4)Review Sessions: To be announced (5) Office Hours
(NLB and 2 TA's) (6) Office hours of other TA's involved in teaching the labs
will soon be announced and are also available to you.
Definitions
Definition: ORGANIC CHEMISTRY--The chemistry of the compounds
of Carbon. .
- For our purposes the "chemistry" being referred
to here is the structure of these carbon compounds and their reactions.
- Structure, in the case of a molecule, is the geometric
description of a molecule, including such things as its shape, size, bond
lengths, bond angles, and dihedral angles.
- A Reaction is the conversion of one molecule into
another.
Review of Atomic Structure
REVIEW OF ATOMIC STRUCTURE
Definitions:
ATOMIC STRUCTURE-- The distribution of electrons in
the space around a nucleus.
MOLECULAR STRUCTURE--The specific, three-dimensional
arrangement of atoms in a molecule.
General Principles:
- Electrons occupy orbitals (atomic orbitals, AO's), e.g.,
1s,2s,2p, etc.which are centered around the nucleus.
- "s" atomic orbitals are spherically symmetric
in shape, p orbitals are dumbbell shaped, etc.
- Orbitals are grouped into concentric shells of orbitals
of comparable energy, e.g., the 1st, 2nd, or 3rd Mainshells, with only one
AO (the 1s AO) in the first main shell, 4 in the 2nd main shell (2s,2px,
2py, and 2pz), 9 in the 3rd main shell, etc.
- The energies of all AO's are negative with respect to the
energy of an isolated, free electron at rest, which is taken as the zero of
the energy scale. The AO energies are negative because the electrons in these
AO's are attracted to the nucleus, making them more stable ( of lower energy)
than free electrons.
- The ionization potential of an electron (IP) is the energy
required to remove it from the nucleus entirely. Since the electron is stabilized
by its attractive interaction with the positively charged nucleus, it requires
energy to remove it. This IP energy is equal to the orbital energy, but with
opposite sign. Thus the IP is positive but the orbital energy is negative.
- The numeral designating an AO (e.g., the 1 in 1s) is a rough
indication of orbital size, the smaller the number for a given atom, the smaller
the orbital. The letter designating an AO indicates its shape, as noted before.
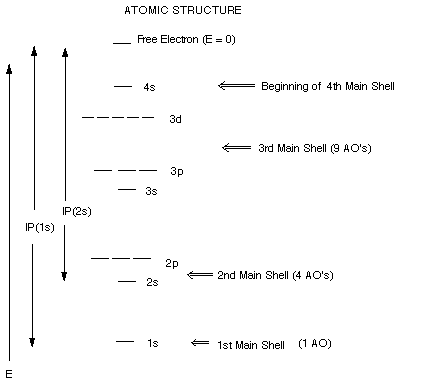
THE ORIGIN OF THE ATOMIC ORBITALS
It is reasonable to ask "Where do we
get these AO's and how do we know their shapes and sizes?" The answer is---
we get them from quantum theory by solving the Schrodinger equation:
Hifi
= Eifi
- Where the Greek letter f is a
symbol for the mathematical function which represents the wave function or
orbital.
- The f's are subscripted because
there are many of them. For example, f1
might be the 1s AO, f2, the 2s, etc.
- Note that there is a specific energy for each wave function
or orbital. For example, f1 has energy
E1, etc. So both the orbitals and their energies, as displayed
on the diagram are obtained from quantum theory.
- H is the energy operator or Hamiltonian, which is specific
to any specific atom, but the general form is specified by quantum theory.
This equation is not especially easy to solve, since it has two unknowns,
the energy and the wave function, and only one known, the energy operator.
- To be more concrete, the 1s orbital for the simplest atom,
the hydrogen atom, looks like this:
fi
= the 1s AO = Nexp(-r/ao)
Where the only variable is r, the distance from the electron
from the nucleus. The a0 is the so called Bohr radius, a constant,
and the N is a constant, called the normalization factor. The key point to remember
here is that the orbital is spherically symmetric, because its value does not
depend on direction ( x, y, or z axis), but only on the distance from the nucleus.
- Very Important:
The electron density or the probability of finding an electron
in a given place is equal to the square of the wave function--- not
the wave function itself. Consequently, since both 1 and -1
give the same square, the absolute sign of the wave function does not
matter.
- Also Important: Not all wave functions or orbitals
are spherically symmetrical, only the "s" type AO's. For example
the 2p AO of hydrogen has a dumbell shape and "points " in a
specific direction, for example the X, Y, or Z axis. It has two lobes,
and the signs of this mathematical function are opposite in each lobe.
Note that the absolute signs are again of no relevance, but the relative
ones are.
2Px AO
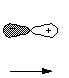 X
axis
X
axis
- Note also that where the sign of the orbital changes from
plus to minus, the value of the wave function is zero (namely at the nucleus),
i.e., the probability of an electron being here is zero. This is called a
node in the wave function. Please note: the signs given here are not
charges!
Ground State Electronic
Configurations of Atoms
DEFINITIONS:
- GROUND STATE--THE LOWEST ENERGY STATE OF A CHEMICAL
ENTITY (ATOM OR MOLECULE)
- EXCITED STATE-- ANY OTHER, HIGHER ENERGY , STATE
OF AN ATOM.
The Hydrogen Atom
- There is just one electron on the hydrogen atom. Potentially
, it could "occupy" (note the language) any of the available orbitals.
The lowest energy state, i.e., the ground state is obtained when the electron
occupies the lowest energy orbital-- the 1s AO. Consequently, in the ground
state hydrogen atom, the electron density of the atom is just that in its
1s AO. So the electron density in the H atom is spherically symmetrical. The
IP of the hydrogen atom is precisely the value predicted from the energy of
the H 1s AO.
- Under most conditions, all hydrogen atoms would prefer to
exist in the lowest energy state.
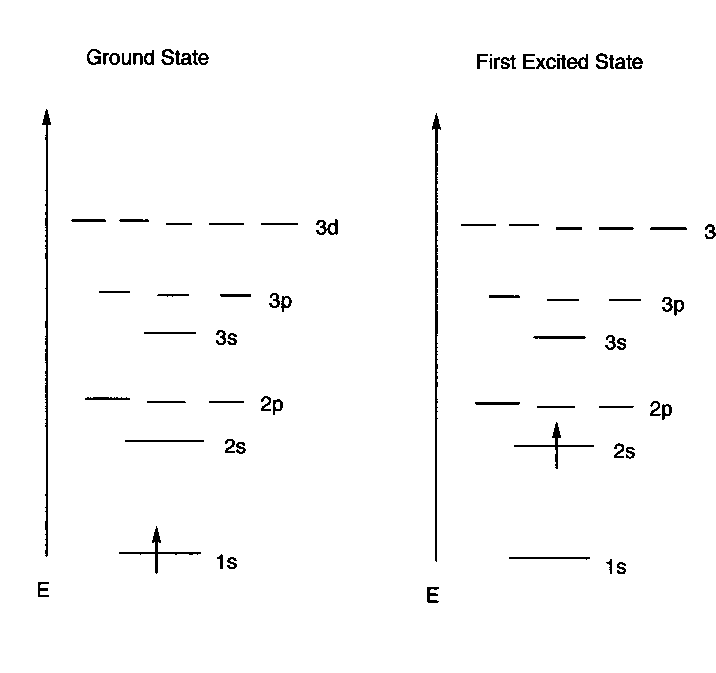
The Electronic Configuration of an Atom: A complete
specification of the all the AO's of an atom which are occupied.
- The Energy Level Diagram Format: A description of
the electronic configuration of an atom using a drawing as shown above for
the H atom. This includes the relative spins of the electrons.
- The "Linear Format": An abbreviated description
of the electronic configuration of an atom which displays the orbitals occupied
and their occupancy numbers, but not the energies of the orbitals, e.g.:
For the ground state H atom: 1s1
(This means that there is one electron ( the
superscript gives the occupancy number) in the 1s AO) .
For the excited state depicted previously:
2s1
(This means that there is one electron in the
2s AO.)
GROUND STATE ELECTRONIC CONFIGURATIONS OF
OTHER ATOMS
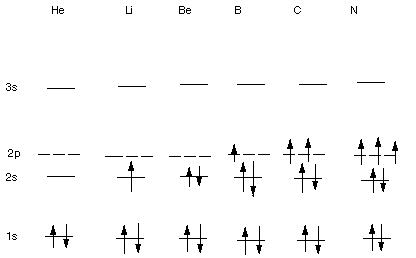
The Linear Format:
He 1s2; Li 1s22s1; Be 1s22s2;
B 1s22s22px1; C 1s22s22px12py1;
N 1s22s22px12py12pz1
etc.
The
Rules for Deriving Ground State Electron Configurations:
- The Aufbau Rule: The electrons are supplied to the
orbitals starting from the lowest energy (1s) orbital and moving progressively
to higher energy.
- The Pauli Exclusion principle: No more than two electrons
can occupy the same orbital. Two electrons occupying the same orbital must
have paired (opposite) spins.
- The Hund Rule: This applies to situations in which
the Aufbau Rule is not applicable, i.e., when two or more orbitals of equal
energy are available. Essentially, the rule states that electrons should be
filled into different orbitals and with their spins unpaired
(i.e., parallel).
Examples:
- For He, the first electron goes into the lowest energy orbital,
1s, in accord with the Aufbau Rule(lowest energy orbital filled first). The
second electron goes into this same orbital (Aufbau) and with spin paired
to the first one (Pauli Exclusion).
- For Li, the third electron goes into the 2s AO, by the Aufbau
Rule.
- For Be, the fourth electron goes into the 2s AO (Aufbau),
and with spin opposite to the other electron in the same orbital (Pauli Exclusion).
- For B, the fifth electron then goes into any one of the
three degenerate (i.e. equal-energy) 2p AO's.
- For C, the sixth electron then goes into one of the other
2p AO's (Aufbau and Hund) and with the same spin as the fifth electron (also
the Hund Rule).
- For N, the seventh electron again goes into a different
2p AO with the same spin as in the fifth and sixth electrons (Hund Rule).
- For O, the eighth electron must go into one of the three
2p AO's(Aufbau), with spin paired to the other electron in the same orbital(Pauli
Exclusion).
- For F, the ninth electron goes into a second 2p AO and pairs
up with the electron already in that AO.
- For Ne, the tenth electron fills up the second Main Shell.
- For Na, the eleventh electron goes into the 3s AO (Aufbau).
- The remaining atoms of the third row of the periodic table
then follow the same pattern as the second row, using the 3s and 39 AO's.
***Note: You should be able to do both energy level
diagram and linear format representations of the electronic configurations of
the ground states of all atoms from H through Ca.
Molecular
Bonding: Ionic
Definition: IONIC BONDING: Bonding which arises
from the electrostatic attraction of oppositely charged ions, as in Na+
F-.
***You should be able to illustrate, using either the linear
or energy level diagram formats, the formation of an ionic bond between two
atoms:
Na 1s22s22px22py22pz23s1
+ F 1s22s22px22py22pz1
Na+ 1s2
2s22px22py22pz2
F- 1s22s22px22py22pz2
Question: Since both the sodium ion and the
fluoride ion have the same electronic configuration, how do they differ?? (The
larger nuclear charge for the sodium ion than the fluoride ion).
- Note that removing an electron from Na requires energy (the
IP of the 3s AO of sodium). Putting that electron in a 2p AO of fluorine supplies
some of the necessary energy, but not all (the electron affinity of atoms
is generally less than the ionization potential). The energy required is supplied
by the ionic bonding which results.
- The example given above illustrates the OCTET
RULE: Na originally had 1 electron in its outermost shell (called the
VALENCE SHELL), while fluorine had 7. Transferring
an electron from sodium to fluorine gives both eight electrons in the outermost
shell.
- Definition: The OCTET
RULE: Atoms or ions (any chemical species) with eight electrons
in the outermost (valence) shell are especially stable.
- Generally speaking, ionic bonding occurs between atoms
in the 1st or 2nd Groups of the periodic table (i.e. atoms which have one
or two electrons in the outermost shell) with atoms of Groups 6 or 7, that
is, atoms which lack only one or two electrons of having a stable octet structure.
- ***Note that the first shell contains only one AO, so
that it is filled up when the occupancy is two. The second shell is , however,
filled when there are eight electrons ( there are 4 AO's). Thus, the octet
rule. However, the 3rd Main Shell also has 3d AO's and so is not completely
filled when it has eight electrons; it could have as many as eighteen. However,
the octet rule still is useful even if not rigorously valid here, because
the 3d AO's are very much higher in energy than the 3p's, so that the third
shell "feels" essentially filled when the 3s and 3p AO's are filled.
Molecular
Bonding:Covalent
Definition: Covalent Bonding --- Bonding resulting
from the sharing of electrons (usually two electrons).
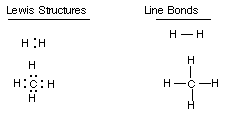
Representations of Covalent Bonds:
A covalent bond may be represented as a pair of
dots between two atoms (a Lewis structure)or as a line drawn between the two
atoms (line or dash bonds).
An unshared electron pair can be represented
as a pair of dots on a single atom.
- A Quantum Theoretical Picture
of Covalent Bonding
Molecular
Orbital Picture of the Covalent Bond
Definitions:
Molecular Orbital (MO): A wave function or orbital
which extends over more than one atom, i.e., a wave function for a molecule.
The symbol for a molecular orbital (wave function) is usually y
, i.e., the Greek letter psi.
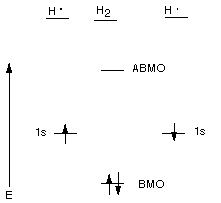
Bonding Molecular Orbital (BMO): An MO which is lower
in energy than either of the AO's from which it is derived. The BMO of the hydrogen
molecule is much lower in energy than the energy of a hydrogen 1s AO.
Antibonding Molecular Orbital (ABMO): An MO which
is higher in energy than either of the AO's from which it is derived.
Description of the Energy Level Diagram:
When two hydrogen atoms, each of which has a single electron in a 1s AO, come
close to each other,the two AO's overlap and delocalize and lose their
identity as AO's. The new orbitals are delocalized over both hydrogen atoms
(they are attracted to both nuclei), i.e., over the whole molecule, are therefore
called MO's. Instead of having two atomic orbitals, we now have two molecular
orbitals. One of the MO's is lower and one higher in energy than the original
AO's. The one which is lower in energy is called the BMO, while the higher
energy MO is called the ABMO. All of the rules we learned about AO's
also apply to MO's, they are still wave functions or orbitals. Since the BMO
can accomodate two electrons, the ground state of the hydrogen molecule
corresponds to the state where the BMO is doubly occupied. Of course, the electrons
must have their spins paired. So we are using the Aufbau and Pauli Exclusion
Principles. Since both electrons are in an orbital which is much lower in energy
than when they are in the 1s AO of a hydrogen atom, they molecule is much lower
in energy ( we say, more stable) than the two separate atoms. The results shown
in the diagram above come from a quantum mechanical calculation using the Schrodinger
equation, but of course the exact energies are obtained, as well as the mathematical
expressions for the BMO and the ABMO.
An Orbital Picture of MO Formation
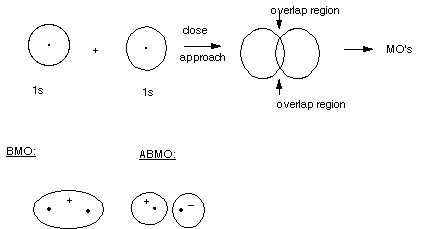
- The BMO has only one lobe, i.e., it has the same sign throughout.
Again, the absolute sign makes no difference , it can be plus or minus.
- We can view this MO as having resulted, in our quantum calculation,
from the combination of two 1s AO's having the same sign. When they overlap,
the bonding region in the center of the bond is enhanced by the addition of
the two AO's, resulting in strong bonding.
- The ABMO has two lobes, these of opposite sign. Again, whether
the plus is on the right and minus on the left, or its reverse is not significant,
but the relative signs of the orbitals in the two lobes is significant. In
the bonding region between the nuclei, the functions are subtractive, resulting
in a node in the bonding region. Since there is no electron density in the
bonding region, the energy is very high.
- We can view this MO is having arisen by the subtractive
combination of two 1s AO's, one having a plus sign and one a minus sign.
- Again, the signs are not charges, but represent the sign
of the mathematical function which represents the orbital.
- When two AO's of the same sign overlap. The overlap is termed
"positive overlap". This can be plus/plus or minus/minus
(absolute signs are irrelevant). When two AO's of opposite sign overlap, the
overlap is termed "negative overlap".
- In general, positive overlap corresponds to bonding and
negative overlap to antibonding.
Requirements
for Strong Covalent Bonding
1.Strong, net overlap of orbitals.
2. Two paired electrons.
Explanation:
- Overlap of atomic orbitals results in their interaction
to form MO's. The stronger the overlap interaction, the greater the lowering
of the BMO ( and the greater the increase in energy of the ABMO).
- The strongest bonding results when the low energy, BMO,
is fully occupied. The maximum occupancy , according to the Pauli Exclusion
Principle, is two and the two electrons must by paired, i.e., having opposite
spins.
- Net bonding can result when there are 1 or 3 electrons in
a bond, because in each case there are more electrons in the BMO than in the
ABMO. When there are 4 electrons, no bonding occurs.
Examples:
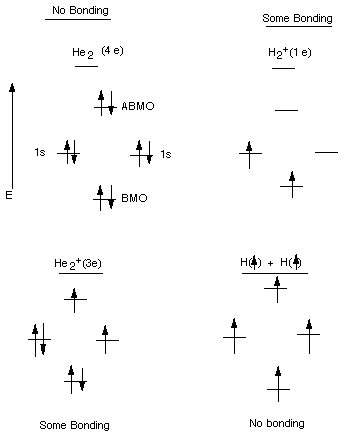
Example 1: Helium atoms , atomic number 2, have 2 electrons
in a 1s AO. When two of these try to combine, the bond has to have 4 electrons.
Two can go into the BMO, but two must go into the ABMO. The ABMO is just as
antibonding as the BMO is bonding, so no net bonding results. Helium atoms do
not form stable helium molecules.
Example 2: This represents the combination of a proton
with a hydrogen atom. The proton has zero electrons, the hydrogen atom has 1
e in a 1s AO. The resulting ionized hydrogen molecule can accomodate the electron
in a low energy BMO, resulting in net bonding, but since there are not two electrons
in the BMO, the binding is less than for the hydrogen molecule (approximately
half).
Example 3: This represents an ionized Helium molecule, with
three electrons. Since two can go into the BMO, only one has to enter the ABMO.
The net result is weak bonding.
Example 4:This represents the attempted combination of two
hydrogen atoms having electrons of the same spin (unpaired). The overlap of
orbitals occurs when the atoms approach each other, and MO's are formed, but
the two electrons cannot enter the BMO. The result is no net bonding.
Hybridization
States of Carbon
HYBRIDIZATION: The mixing of atomic orbitals, such
as s and p orbitals, to form a new, hybrid orbital for use in bonding.
- Carbon virtually never uses a pure s orbital to bond.
- Carbon has three different ways that it hybridizes. These
are designated sp3, sp2, and sp. In the first case,
all three p orbitals are mixed in with the s orbital. In the second case,
only two of the p orbitals are mixed in, and in the sp case only one p AO
is mixed with an s orbital. The designation sp3 is intended to be a shortened
form of s1p3.
Tetrahedral
Hybridization
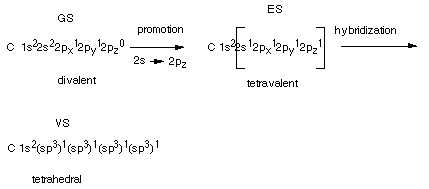
The way in which the sp3 hybrid AO's are arrived
at can be viewed conceptually as follows. Start with the ground state(GS)
of atomic carbon written in either the linear or energy level diagram format.
Consider the formation of an excited state (ES) of carbon by the promotion
of an electron from the 2s to the 2pz (the z should be a subscript) AO. With
respect to bonding to hydrogen atoms or other atoms, the GS is only divalent
because it has only two half-filled AO's which could be used to form covalent
bonds to hydrogen atoms.In contrast, ES is tetravalent, i.e., it can
bond four H atoms using the four half-filled AO's. Each C-H bond lowers the
energy by about 100 kcal/mol, so the two additional bonds lower the energy by
200 kcal/mole relative to the two bonds formed by the
GS. The excitation energy, i.e., the energy required to promote an electron
from the 2s to the 2p AO is 96 kcal/mol. So that the extra 200 kcal/mol provided
by the two additional bonds is more than enough to make the overall transaction
favorable. Note that the promotion itself is unfavorable, but once the atom
has bonded to form CH4, the overall result is more favorable using
the ES than the GS.
However, carbon does not exactly bond via this ES, either.
The ES has two different kinds of AO's available for bonding, and if these were
used, they would give rise to two different bonds in methane. In fact all four
bonds are exactly equivalent, and all four H's are equivalent. The second and
final step in arriving at the Valence State (VS) is hybridization of
all four of the valence shell orbitals to form four equivalent AO's, called
tetrahedral or sp3 AO's.
Tetrahedral bonding:
a specific type of tetravalent bonding in which the valence are directed
to the four corners of a tetrahedron. The bond angles are approximately 109.5
degrees.
Note that in the mixing process, all four valence shell orbitals
(but not the inner shell orbital) are mixed together into one grand wave function
which is divided into four equal parts. Again, we could ask "where does
the idea for a tetrahedral orbital come?" Basically, again from quantum
theory but also from experimental observation of equivalent H atoms in methane
and the tetrahedral angle in methane and in analogous hydrocarbons (alkanes).
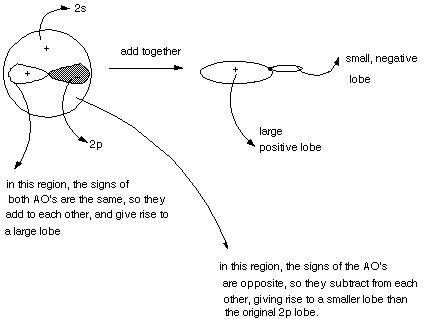
Shapes of Hybrid Orbitals. All hybrid AO's are basically
very similar in shape. They are like the p orbitals in that they have two lobes
and are oriented in a specific direction, i.e., they point toward a nucleus
to which they are bonding. However, they are unlike p orbitals in that the "size"
of the two lobes are unequal. The origin of the shape of a hybrid orbital is
most easily illustrated by the mixing of a single 2p AO with the 2s AO, to give
an sp hybrid AO.
Hybridization
of Other Atoms
The Hybridization States of Other Atoms. It
is not only carbon which bonds using hybridized AO's. Most other atoms do, too.
Consider oxygen and nitrogen as familiar examples.
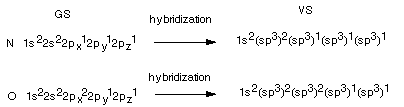
- Note that in these cases, excitation would not increase
the valence, which for N is 3 and for O is two. Hybridization proceeds
directly from the GS.
The Reasons
for Hybridization
Why does Hybridization Occur? Two primary reasons
can be given:
(1) The hybridized orbitals provide better overlap and stronger
bonding because like a p orbital they are oriented toward a specific nucleus
in bonding, but they are superior to a p orbital in that they do not "waste"
a lobe of equal size to the one generating the bonding.
(2) Spatially, the 2p and 2s orbitals occupy very similar
volumes of space. It is virtually impossible for another atom to overlap with
one of them without also simultaneously overlapping with the other.
The
Trigonal Hybridization State
The sp2 Hybridization State. Consider
boron:

- Note that promotion increases the maximum valence from one
to three, so that excitation is feasible.
- Note also that only two of the 2p orbitals are mixed in,
the third is not. That is because the third orbital is vacant and is not involved
in the bonding.
- The mixing of two 2p's with a 2s gives the sp2
hybridization state, which is also called the trigonal hybridization state.
- Since the 2pz AO is not mixed in, the hybrid
orbitals lie in the xy plane.
- Since the three hybrid orbitals lie in a plane and they
are all equivalent, the bond angle is 120 degrees. The planarity and the 120
degree bond angle are both key aspects of trigonal hybridization.
- One could ask," Why is the 2pz the AO which
is omitted from hybridization?". The orbital which is omitted is the
one which is vacant. It could have equally well been any of the 2p AO's, but
it could not have been the 2s, since because of Aufbau, the 2s orbital must
be occupied. Essentially, the orbital is left vacant which has the highest
energy.
Trigonal Hybridization of Carbon. Carbon can
also be trigonally hybridized under two different sets of circumstances: (1)
When it is isoelectronic with boron and (2) When it is doubly bonded to another
atom (any atom which can form two valencies).
Definition: Isoelectronic
species--- two chemical species which have the same number
of total electrons or the same number of electrons in the valence shell.
Example: Boron atoms have 5 electrons and carbon atoms have
6. Positively charged carbon cations have one less electron and thus are isoelectronic
with B. Similarly, negatively charged boron is isoelectronic with neutral carbon
(both have 6 e). Positively charged nitrogen is isoelectronic with neutral carbon.
The Isoelectronic Principle
- The Isoelectronic Principle: Species which
are isoelectronic tend to have the same ground state electronic configurations,
the same first excited state configurations, and the same valence state configurations.
They therefore have the same hybridization state in bonding.
- As an exercise, show that the GS, ES, and VS are identical
for the following pairs: neutral B and positively charged C; negative B and
neutral C; positively charged N and neutral C.
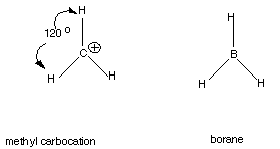
Carbocations
Carbocations: The family of trivalent,positively
charged carbon species is called the "carbocation" family. The
simplest example is the methyl carbocation:
Hybridization in Alkenes
ALKENE STRUCTURE
Doubly Bonded Carbon: Neutral carbon atoms can
also hybridize trigonally if the carbon is bonded to only three atoms. In this
case the third, unhybridized p orbital(which is now singly occupied) is used
to form a second bond ( a pi bond) of a novel type to one of the three atoms.
An extremely important case is that in which carbon doubly bonds to another
carbon atoms, as in the molecule ethene. In this molecule, both carbon atoms
are trigonally hybridized and each is bonded to to other hydrogen atoms.
- The three hybrid AO's are used to form what are called sigma
bonds to three atoms, thus each carbon atom forms a sigma bond to two hydrogens
atoms, and one to the other carbon atom.
Sigma Bonds
- Definition: A Sigma Bond: A bond formed by the
overlap of orbitals which "point at" each other. The bond is cylindricallly
symmetric about the bond axis ( the line drawn between the two nuclei).
- The sigma bonds in ethene are shown below:
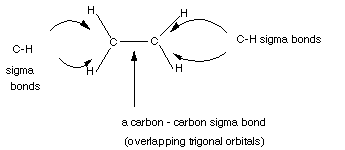
This is the sigma framework of ethene. But remember that each
carbon has a 2p AO left over, unhybridized, which is singly occupied and thus
able to form another bond, if everything is set up for overlap. Below the VS
for neutral carbon in a situation for forming a double bond is shown:
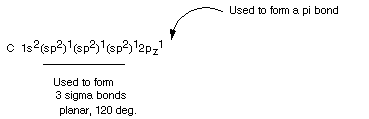
Pi Bonds
The fourth valency for each carbon atom is then filled
by forming a pi bond between the two carbon atoms, using the overlap of the
2pz AO's on each carbon. Thus the carbon atoms are joined be two bonds, this
being called a double bond, but one bond is a sigma bond and the other a pi
bond.
Note that although the carbons are tetravalent--i.e., they
have four bonds each-- they are only bonded to three atoms. This is the situation
in which carbon typically uses trigonal hybridization.
DEFINITION: A
Pi Bond is a bond formed by sidelong or lateral overlap of two p type orbitals
(not by end-on or sigma type overlap).
The Digonal Hybridization
State
DIGONAL HYBRIDIZATION. When carbon is bonded
to only two other atoms it needs, to complete a tetravalency, to form a triple
bond to one of these atoms (or double bonds to both of them; see later). A
triple bond consists of a sigma bond plus two pi bonds. If you recall, a
pi bond requires the overlap of two p type orbitals in a "lateral"
or sidelong fashion. Since carbon in this situation must form two pi bonds,
it must leave two 2p AO's unhybridized, so that only one is mixed in:
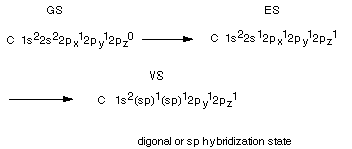
- Note that only one of the 2p orbitals is mixed with
the 2s orbital, and that two pure, unmixed 2p orbitals remain to form pi bonds.
- Also note that, in our example, only the 2px AO is mixed
in, so that the digonal orbitals have no y or z component in their directionality.
They both must be directed along the x axis. How can this be? One is directed
along the positive x direction and one in the negative x direction. The angle
between them is 180 degrees--they are linear.
- The two sigma bonds are formed using this digonal orbitals.
The sigma framework of ethyne, the simplest organic compound having a triple
bond, is shown below.
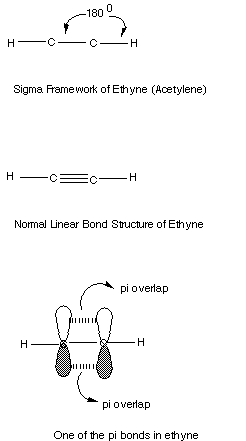
Note that the second pi bond is perpendicular to the first.
It will use the py orbital, while the first pi bond, in our illustration,
used the 2pz AO's.
BACK TO THE TOP
ON TO THE NEXT PAGE
BACK TO THE TABLE OF CONTENTS
BACK TO THE BAULD HOME PAGE
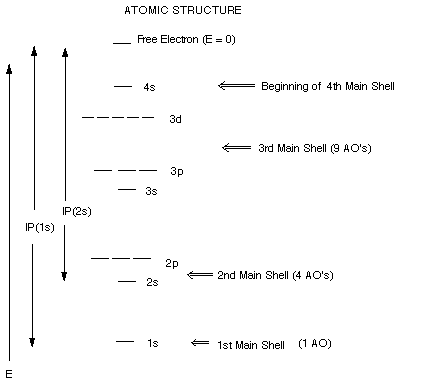
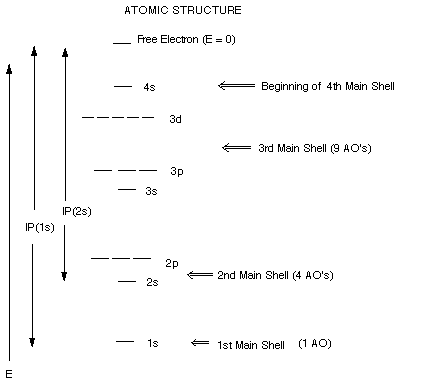
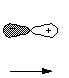 X
axis
X
axis
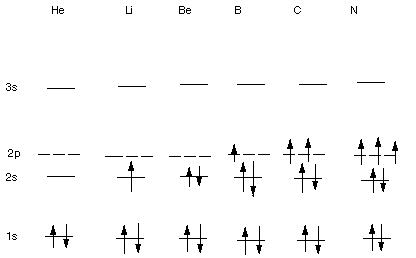
![]()