ALKENES II: REACTIONS OF ALKENES

TOP

TABLE OF CONTENTS FOR THIS PAGE

Reaction types
Reaction Mechanisms
Transition State Theory
Reaction Path Diagrams
Reaction Rates and Rate Constants
An Example of a Reaction Mechanism
Reaction Path Diagram For this Example
Transition States
Transition State Models
Resonance Theory of Transition States
Regiospecificity and Competing Transition States
Relative Rates of Addition to Different Alkenes
Stabilization of Carbocations by Alkyl Groups
Transition State Refinement: The Hammond Postulate

REACTION TYPES

Organic reactions are classified as to Reaction Type based upon the overall changes which occur in the product as compared to the reactant(s).

For alkenes the distinctive reaction type is Addition.

This is because the pi bond of an alkene can be broken and this bond replaced by bonds to other (external) agents. For example, ethene can add molecular hydrogen to give ethane. In this reaction, two reagents add together to give a single product. This is typical of the type of reactions that alkenes undergo.

Alkenes are especially reactive because the pi bond is relatively much weaker than a sigma bond.

In contrast, alkanes cannot undero addition at all, because the carbons of an alkane already have the maximum number of atoms (four) bonded to them. They therefore cannot add another atom. For example ethane can not add more hydrogen . Substitution, where, for example, a hydrogen atom of an alkane is replaced by some other atom or group, such as a halogen atom is the typical reaction.

The symbol for an addition reaction is "Ad", wherease that for a substitution is "S".

REACTION MECHANISMS

A Reaction Mechanism is a stepwise description of the reaction path. In our course this will consist of a set of chemical equations along with certain other specifications (to be specified later) such as the rate determining step.

The term Reaction Path refers to the lowest energy pathway from the reactants to the products, i.e., the one which is actually preferred and followed in a chemical reaction. Many paths are conceivable, but the easiest and fastest way to convert reactants to products is via the lowest energy path.

The importance of knowing the mechanism of a reaction lies in the ability to (1)exert some control over the reaction in regard to its rate and yield, and in general its efficiency and (2) the ability to predict the precise stereochemistry and other subtle aspects of the structure of the product.

In our discussion of reaction mechanisms, we will designate a general reactant or group of reactants as "R" and the product of this general reaction as "P".

Some reactions occur in a single elementary reaction step. That is, all of the bonds which are to be broken in the reactant and all of the bonds which are to be formed in the product are broken and formed in one step. Such reactions are called "Concerted Reactions".

Most reactions occur in two or more steps (possibly many). Such reactions are called "Stepwise Reactions". In a stepwise reaction, the formation of intermediates (to be defined) is involved.

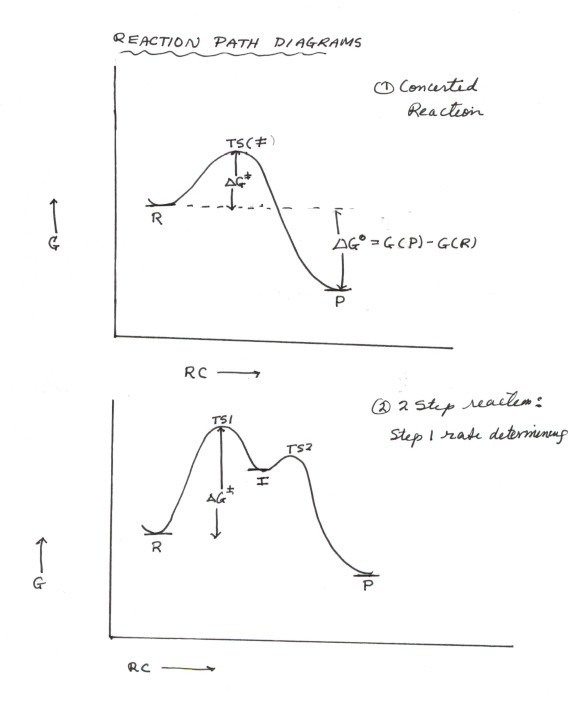
TRANSITION STATE THEORY

Consider a simple, one-step reaction. The reactant R is converted to the product P by breaking one or more bonds of R and forming one or more new bonds as found in P. The process of breaking bonds thus requires energy, so nearly all reactions require some input of energy, called activation energy.

This can be illustrated by considering what we call a Reaction Path Diagram, which plots the energy (usually in uncalibrated units) on the vertical axis versus the Reaction Coordinate, which is a measure of the progress of the reaction from the geometry of R toward that of P. The point of highest energy on this reaction path is called a Transition State.

Formally, a transition state is defined as the state of highest energy on the lowest energy reaction path. An important consequence of this definition of the TS is that the energy difference between the transition state (abbreviated as TS or as a double dagger) and that of the reactant(s) is the activation energy. We will see that this activation energy controls the rate of the reaction: the lower the activation energy, the faster the reaction goes, and the higher the activation energy, the slower the reaction goes.

Various energy parameters can be used on the vertical axis. We will start out by using the quantity G, the Gibbs free energy, because rigorously this is the quantity which actually controls the rate. Other options are the enthalpy H or the chemical energy,E, which are less directly related to the rate.

It is important to note that the (1)the energy difference between the R and P controls the thermodynamic equilibrium between R and P and that (2)the energy difference between the TS and R controls the rate of the reaction. An important consequence of this is that the energy of the product does not directly enter into the quantity (activation free energy) which controls the rate of a reaction. However, the TS energy obviously cannot be less than that of the P.

In a two step reaction, illustrated in the second diagram below,there is an intermediate state which, like the reactant and product, is an energy minimum. This state is designated as I on the reaction path diagram . The formal definition of an intermediate is an energy minimum encountered on the reaction path between R and P . The physical significance of being an intermediate, as opposed to a TS, is that a substance which exists at an energy minimum has a significant lifetime and, in many cases, its presence can be physically detected and its reactions chemically diverted if desired to another course. A TS is so short lived that it cannot be detected by conventional physical means, and its chemistry cannot be affected by any other reagent.

In a two step reaction, there are two extreme scenarios, i.e., either the first step is rate determining (we call such a step the rate determining step or rds) or the second step is rate determining.(By extreme we mean that possibly neither step will be rigorously rate determining). The scenario illustrated below is one of the former type in which the first step is rate determining. The concept of a rds is extremely important in dealing with reaction rates of organic reactions. It is defined as a reaction step the rate of which is equal to the overall rate of the reaction. The importance of the concept is this: If the rate of a single step is exactly equal to the overall rate of product formation (or of reactant consumption, which should be the same thing), anything we know about the rate of this step will immediately help us to know about the rate of the overall reaction. Thus, if a reaction has 10 steps and one of them is rate determining, we really don't need to know anything about the rate of 9 of them, if all we are interested in is the rate of the overall reaction. Conversely, anything we learn about the overall reaction rate immediately tells us about the rds and it alone.

The reasons why the first step in the illlustrated diagram is the rds are twofold: (1)Once the intermediate I is formed, it virtually always goes on to product, as opposed to returning to the starting materials (reactants). Why is this? Simply look at the height of the two barriers separating I from P and from R. Note that the barrier for return to R is substantially higher than that separating I from P. So the rate of return to R is much slower than the rate of conversion to P. (2) The second requirement is that the concentration of the intermediate must not build up, i.e., I is very quickly converted to P, so that there is very little hold up. Thus, the overall picture is that I essentially never returns to R and it doesn't buld up, but goes quickly over to P .So, as fast as I is formed it is conerted to P. That makes the rate of formation of I essentially equal (for all practical purposes, equal) to the rate of formation of P.

If the second step of the reaction is rate determining, this corresponds to the first step being an equilibrium. That is the intermediate rapidly goes back to R and only slowly on to P. In such a case, the activation energy for the reaction is the energy difference between the transition state of higher energy (in this case the second TS) and the R. See if you can draw a reaction path diagram which proprerly shows that I goes back to R faster than it goes on to P.

REACTION PATH DIAGRAMS

Reaction Rates and Rate Constants

Consider an elementary reaction step such as the one shown below:

The rate of the reaction is the rate at which P is formed or R is consumed. This can normally be measured experimentally by simply analyzing the amount of R present at various times.

The rate is proportional to the concentration of R to the first power, since the more R we have, the faster P is formed.

The proportionality constant, designated as k (small k, to distinguish it from the equilibrium constant K), is called the rate constant. We should make a very clear distinction between the rate of a reaction (the overall rate) and its rate constant. The rate constant is a measure of the reaction rate at unit concentration of the reactant, so that it is a measure of the inherent speed of the reaction, and is independent of the concentration of the reagent. Any reaction can be speeded up by increasing concentrations of reagents, but this doesn't affect the rate constant.

It is this measure of the inherent rate of a reaction which is related directly to the free energy of activation. The larger the activation free energy required, the smaller the rate constant.

Again, if a given step of a multistep reaction is the rds, the rate of the overall reaction giving the final product is still equal to the rate of this step. So the rate law for this single step gives the rate law for the overall reaction.

For any reaction, be it a single or multi-step reaction, the expression which gives the overall rate of the reaction in terms of rate constants and concentrations of reagents is called the Rate Law.

An Example of a Reaction Mechanism: Addition of HCl to An Alkene

CONSIDER THE ADDITION OF HCl TO ISOBUTENE

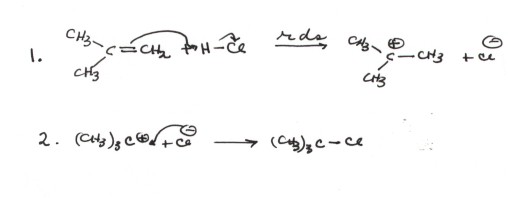
IMPORTANT NOTES ABOUT THIS MECHANISM

First, please note the format and conventions of writing mechanisms. You must always write the different steps of a mechanism on separate, numbered lines.

You must always designate, if known, the rds. Also, if any step is an equilibrium, this must be indicated by the use of equilibrium arrows.

You must show by means of arrows the flow of electrons into the new bonds. In the first step, the electron pair of the pi bond flows toward the hydrogen of HCl to form a carbon-hydrogen bond to one of the alkene carbons, the other being left then with a positive charge (as a carbocation). Since hydrogen cannot be divalent, the electron pair of the H-Cl bond must flow onto the chlorine atom, generating a chloride anion. In the second step, the electron pair on the chloride anion flows toward the carbocation center to form a C-Cl bond.

In this reaction, the overall result is the addition of HCl to isobutene. The tert-butyl carbocation is an intermediate. Being very reactive, it doesn't build up, but always goes on to the product. The first step is the rds, while the second step is fast and not reversed.

You should be able to explain why the first step is the rds.This is really quite simple. The second step breaks no bonds and forms a bond. It is therefore very favorable energetically ( it has a negative delta G) and because no bonds are broken, it is very fast. However, in the first step two bonds must be broken, and only one is formed. The breaking of two bonds is in itself difficult, and in this case the reaction is also energetically very uphill (unfavorable) because only one new bond is formed in the first step. In general, with reasoning like this (simply noting how many bonds are broken and formed), you can adequately rationalize or even predict which step of a reaction will be the rds.

Finally, please note that the carbocation intermediate is very reactive because in it the carbocation center is only trivalent and it can therefore readily form a new bond without breaking any bonds. It is a strong Lewis acid.

A REACTION PATH DIAGRAM FOR THIS REACTION

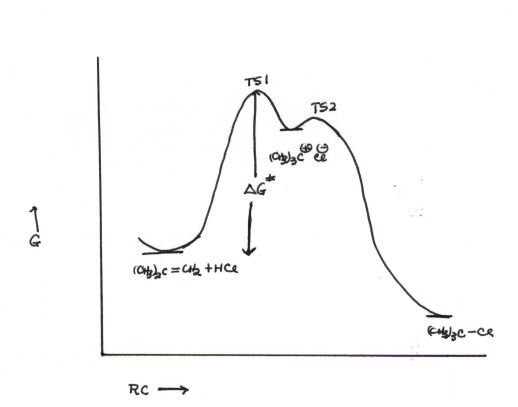
THINGS TO NOTE ABOUT THIS RP DIAGRAM

Note that, overall in this reaction, two bonds are formed (C-H and C-Cl) and two are broken (the C-C pi bond and the H-Cl bond), but these are not all broken and formed at once. The lowest energy reaction path involves breaking two of these bonds and forming one in the first step.

Again, note that an intermediate is an energy minimum. This is the tert-butyl carbocation/chloride ion pair. Note that in the drawing, the barrier to going on to the product (second step, via TS2) is smaller than the barrier to going back to the reactant (via TS1). So the intermediate always goes on to product , and the first step is rate determining.

Note that the activation free energy is that of the first step, since it is rate determining. No further activation is required, since the intermediate always goes on to prodcuct, and never builds up in concentration.

So, although there are two steps and two TS's, the second one is of no consequence as far as the rate is concerned

TRANSITION STATES AND TS MODELS

THE NATURE AND IMPORTANCE OF TRANSITION STATES

Transition states have extremely short lifetimes (less than about 10 ^-13 seconds), so they are extremely difficult to detect. We therefore have very little experimental knowledge about them. They exist for so short a time (usually the time required for the vibration of a bond) because they are at the top of the energy curve and require no further activation to go on to product.

Nevertheless, TS's are extrememly important, especially in the context of reaction rates (they are irrelevant in the context of equilibria; why?) because the energy of the TS relative to the reactant determines the energy barrier, which in turn determines the rate of the reaction.

Therefore, it is important that we have some information about them, even qualitative information, in order to organize our knowledge about the reaction and especially to be able to make some predictions about relative rates.

Transition State Models

For the above reasons,it is extremely valuable to have even a rough and qualitative structural model of the transition state of a reaction, such as the addition of HCl to isobutene. Such a model would contain information about the magnitude and location of any charge which is generated in the TS, an indication of any bonds which are being made or broken,and other things.

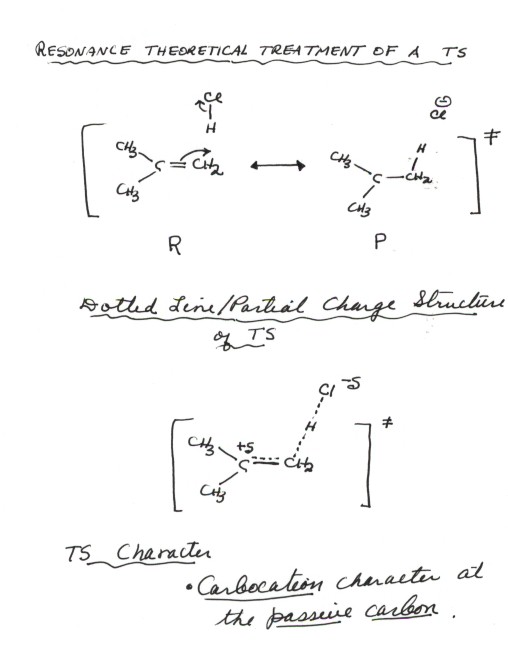
Resonance theory, which we have discussed previously, provides a convenient way to derive a TS model for any reaction. Since a TS is intermediate in geometry between the reactant and product, it should be possible to represent it, using resonance theory, as a resonance hybrid of reactant and product-like structures. In fact, these should normally be the best two canonical structures. It may be necessary, later,to provide additional structures also, but any transition state should be a least reasonably well represented as a hybrid of these two main structures.

In applying resonance theory, it is important to recall that all resonance structures apply to a common geometry, in this case, that of the real TS, even though this may not be precisely known. The important factor here is the two reactants in our case must be oriented at least roughly as we anticipate them to be in the TS. In other words (see the resonance structures below) with the H end of the H-Cl molecule approaching a single carbon of the alkene double bond, since the proton is obviously going to bond to one carbon.

In the case of the first step of the reaction of H-Cl with isobutene, which is the rds, the reactant-like (or R-like) structure is that of isobutene and HCl, properly oriented. The product-like (or P-like) structure is that of the tert-butyl carbocation/chloride ion pair, again properly oriented. If we write the R-like structure properly oriented, we can generate the P-like structure just by electron flow arrows, as shown. These electron flow arrows should be shown when you are using TS theory to derive a TS model.

Dotted line/partial charge (DL/PC) Structures. This completes the first step in deriving a TS model for our reaction step. We can make this easier to analyze by summarizing the resonance theoretical treatment in terms of a dotted line/partial charge (DL/PC) model. This is done simply by representing any bonds which are being made or formed (i.e., any bond which is made in the R and broken in P, or conversely) as dashed lines. These dashed lines imply a Partial Bond. Secondly, partial charge accumulations are represented by +d or -d (lower case Greek delta) at the proper location. Any position which is charged in one structure and not in the other has a partial charge.

Our DL/PC model of the rds of the HCl/isobutene reaction should now show the C-C pi bond as partial, as well as the H-Cl bond, both of which are being broken. It should also show as partial the C-H bond which is being formed. A partial positive charge is on the carbon which is not bonding to the proton. We will call this the passive carbon since it is not being attacked by the proton.

We will see momentarily how this very simple TS model can aid us in thinking about the results of organic reactions, not only reaction rates but products of reactions.

Finally, it wil be important for us to know how to think with these TS models. What aspects or characteristics of the model are likely to yield important insights into the reaction. We call this "Characterizing the TS". In this case, the main character of importance in the TS is THE DEVELOPMENT OF CARBOCATION CHARACTER AT THE PASSIVE CARBON. Note that the character and its location are both specified. Later, we will learn to further refine and extend this TS character.

RESONANCE THEORETICAL TREATMENT OF A TS

REGIOSPECIFICITY AND TS MODELS

Regiospecificity: Let's begin immediately to put the TS model and its character to use. We can do this by considering the regiochemistry of the HCl addition reaction. Note (see illustration) that there are two senses in which HCl could potentially add to isobutene, one which gives the product actually observed, tert-butyl chloride and one which would have led to isobutyl chloride. Essentially,this corresponds to a very high degree of selectivity for the proton adding to the CH₂ end of the alkene and the Cl adding to the other end, as opposed to the opposite situation. This orientational selectivity is called "regioselectivity" or "regiospecificity" (organic chemists can't seem to make up their minds about this) . Of course, this does not even come up in the case of a symmetrically substituted alkene like ethene, or even with isobutene when it reacts with a symmetrical reagent like Cl₂. It only comes into play when two unsymmetrical reagents react.

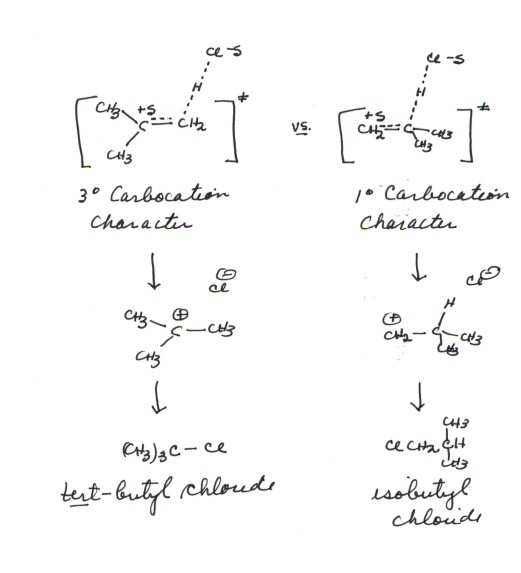
Method of Competing Transition States: Let's now attempt to represent a TS model for each of these two reactions. Since we have already developed the model for the observed isobutene reaction, we don't have to go all the way back and do the same thing for the other regiochemical sense. All we have to do is turn the isobutene around so that the proton is bonding to the more hindered end of the alkene (illustration).The TS models are very similar, except that the carbocation character is being developed in one case at a tertiary carbon and in the other case at a primary carbon. We will thus refine our TS characterization to read "tertiary carbocation character at the passive carbon" in one case, and " primary carbocation character at the passive carbon' in the other.

In a short while , we will learn that tertiary carbocations are much more stable than primary carbocations(and why). Thus, the TS with tertiary carbocation caharacter is much more favorable (lower in energy) than the TS with primary carbocation character. We can thus see why the reaction proceeding via the tertiary TS is much faster, and why the tert-butyl chloride product is essentially the only one observed.

,

TS MODELS RATIONALIZE THE OBSERVED REGIOCHEMISTRY

The general procedure we will use for such comparisons is the METHOD OF COMPETING TRANSITION STATES. We, of course, use TS Models of the TS's of the competing reactions. The lower the energy of a series of competing transition states, the lower the activation energy, and the faster the reaction. The reaction which will be preferred is the faster one, of course.

In the diagram above,the TS which has tertiary carbocation character is of lower energy than that which has primary carbocation character, because positive charge on a tertiary carbon is more stable than ion a secondary or primary carbon. The lower the energy of the TS, the lower the activation energy and the faster the reaction. Thus protonation of the methylene carbon is faster than protonation of the carbon bearing two methyl groups. [Incidentally, there is also a steric factor which favors the approach to the less sterically hindered methylene carbon]

In general, the development of tertiary carbocation character in a TS is more favorable than secondary carbocation character, which is more favorable than primary carbocation character. The least favorable is methyl carbocation character.

The product of the reaction of HCl with isobutene is thus tert-butyl chloride (i.e., 2-chloro-2-methylpropane) and essentially no isobutyl chloride (i.e., 1-chloro-2-methylpropane) is formed. In the case of addition to propene, isopropyl chloride is formed, and no substantial amount of 1-chloropropane (secondary vs. primary carbocation character in this case). The regiochemistry of addition is predicted by a qualitative rule, called the MARKOVNIKOV RULE: : "In electrophilic additions of HX, the proton adds to the less highly substituted carbon atom of the double bond". We can now understand , and we should be able to explain, that this is a result of the development of positive charge on the more highly substituted carbon atom, where the charge is more highly stabilized. (Recall that carbocation character is developed not on the carbon being attacked by the proton, but on the "passive carbon".

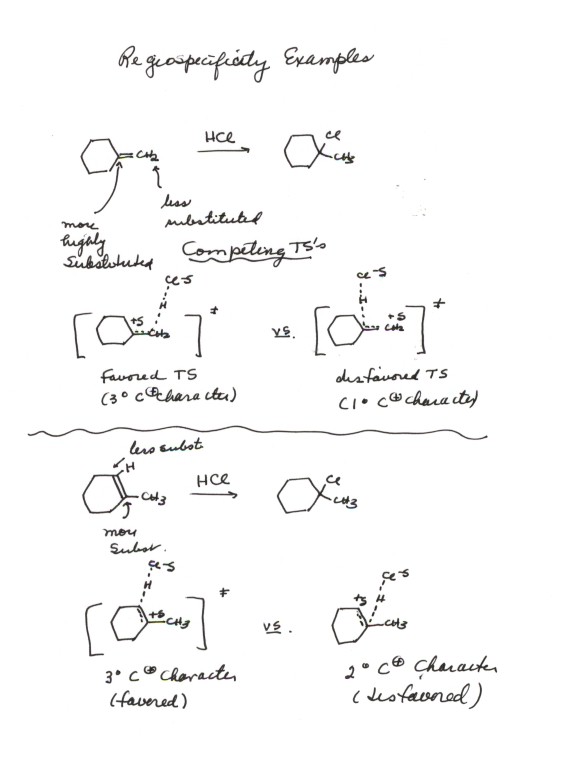
Two other additional examples are provided in the diagram below.You should be able to predict the orientation of the addition of HCl to virtually any alkene using (1)the Markovnikov Rule and (2)rationalize it bY drawing competing transition states for the two modes of addition.

RELATIVE RATES OF HCl ADDITION

RELATIVE RATES OF ADDITION TO DIFFERENT ALKENES

The relative rates of addition of HCl to different alkenes can also be predicted using the same Method of Competing TS's. This is important tool, because the rates of addition to some alkenes may be slow, to others modest, and to others fast. The alkenes which react very slowly may need to be reacted at a higher temperature in order to obtain a reasonable reaction rate. We need to know which alkene we are dealing with and whether to expect its reaction to be fast or slow. This can be especially important when two or more alkene functions are present in the same molecule. We could then predict which one of them will react fastest, and may be able to leave the less reactive one intact.

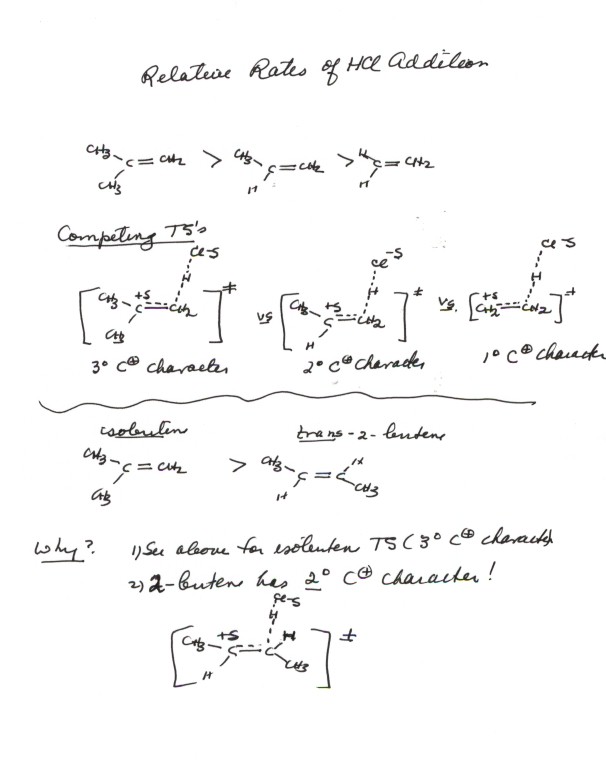
In the reaction series isobutene, propene, and ethene(shown above) the first named alkene reacts very fast, while the last one reacts relatively slowly. Propene reacts at an intermediate rate. Such a sequence of relative rates can be easily predicted or explained, by observing that the TS's for the additions have tertiary, secondary, and primary carbocation character, respectively.

It is important to note, as is also shown in the above diagram, that a disubstituted alkene having both alkyl groups attached to the same carbon, such as isobutene, reacts much more rapidly than a disubstituted alkene having one alkyl group on each carbon, such as 2-butene, because positive charge is developed upon only one of the alkene carbon atoms. Thus, the TS for addition to 2-butene has only secondary carbocation character, the second alkyl group not being at a site of positive charge and exerting little effect upon the reaction rate.

CARBOCATIONS

The Hybridization and Structure of Carbocations has previously been discussed.

The important new point to be added here is that carbocations, though extremely reactive as a class, vary greatly in their stability and reactivity. In particular,the stability order is tertiary>secondary>primary>methyl. The reactivity order is just the reverse. That is, the methyl carbocation is the least stable and the most reactive. The classification of primary, secondary, etc. is made on the basis of whether the trigonal, carbocation center has 1,2, or 3 carbons bonded to it.

The replacement of each hydrogen on the methyl carbocation by an alkyl group furnishes an increment of additional stabilization. We say that alkyl groups stabilize a carbocation center.

The amount of stabilization per alkyl group is approximately 15-20 kcal/mol even in the solution phase. It is much greater than this in the gas phase. The amount of the stabilization is thus relatively large, either in solution or in the gas phase.

The stabilization of a carbocation center by an alkyl group occurs by two distinct means: (1) a resonance effect, specifically, hyperconjugation and (2) an inductive effect.

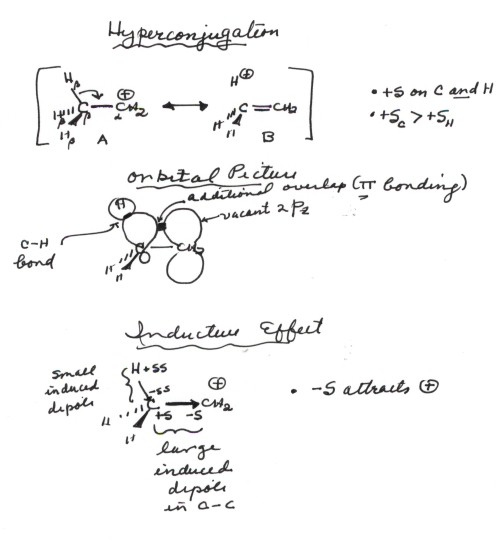
Hyperconjugation. You recall that a resonance effect refers to situations in which a single structure does not adequately represent the bonding and charge distribution in a molecule. The electrons are thus more highly delocalized than in any single canonical structure. A hyperconjugative effect is a specific type of resonance effect in which the delocalization involves a sigma bond. Referring to the resonance structures for the ethyl carbocation, shown below, structure B is also a valid structure which has the same number of bonds as that of A (although they are of different types). Notice that B shows that the positive charge is not localized completely upon the central carbon atom, but is delocalized onto the hydrogens which are beta to the carbocation center. To put it differently, the electrons in the C-H sigma bonds are delocalized onto the carbocation site, forming a partial pi bond between the carbocation site and the attached carbon atoms. The real structure of the ethyl carbocation is thus a resonance hybrid of these two structures and is intermediate between the two. However, since structure A is of lower energy than B, the real structure more closely resembles A than B. Thus, there is more charge on carbon than on H, and the carbocation tends to react more readily at carbon than at H. Note that A is of lower energy than B because a relatively strong C-H bond in A is replaced by a much weaker C-C pi bond in B.

The overlap which gives rise to the resonance stabilization/delocalization is between the 2p orbital on the carbocation center and the sp³ orbital on the beta carbon. If there is no beta carbon, as in the methyl carbocation, this critical overlap is missing.

Each additional alkyl group attached to the carbocation center provides additional delocalization, so that the isopropyl carbocation(which has two alkyl groups) is more stable than the ethyl carbocation(which has just one) and the tertiary butyl carbocation(which has the maximum of three) is more stable than either. Please note that the methyl carbocation has no beta hydrogens to delocalize the charge. Alpha hydrogens can't delocalize the charge, which you can verify by attempting to write good resonance structures for the methyl carbocation (there are none).

The inductive effect which stabilizes a carbocation center results from the induction of a bond diple in the C-C and the C-H bonds by the carbocation center. The positive charge on this carbon makes it very electron deficient, so that it behaves like a very highly electronegative atom and this makes the C-C bond very polar covalent bond, with the negative end at the carobocation center. This partial negative charge is attracted to and stabilizes the positive charge of the carbocation center(the negative potential energy of attraction of opposite charges). Similarly, the positive charge on the beta carbon, makes it somewhat more electronegative than is usual for carbon, and it induces dipoles in the C-H bonds which are oriented with the negative end of the dipole closer to the carbocation center, resulting in a net stabilization. So the inductive effect here refers to the induction of bond dipoles in the neighboring bonds.

REFINING THE TS MODEL: THE HAMMOND PRINCIPLE

Finally, it is important, in the consideration of TS models, not only to be able to discern the qualitative character of the TS, but also to have some idea of the extent to which this character is developed in the TS.For example, in the purely hypothetical case that the addition of HCl to an alkene had only a very minor amount of carbocation character upon the passive carbon, the rates of reaction of isobutene, propene, and ethene might not be very different at all. Further, the rates of protonation of the two non-equivalent carbons of isobutene might not be very different, so that both product regioisomers would be produced in significant amounts. The reaction would thus be said to be relatively "unselective". If, however, there is very extensive development of carbocation character, so that the TS closely resembles a carbocation, we can expect that the reaction will be very selective. Rate differences between various alkenes will therefore be very large, and the regiospecificity of addition to an unsymmetrical alkene will also be high.

The Hammond Principle prodvides an excellent approach to further refining our TS as to the extent of a given character developed in a TS. Essentially, the postulate states that "The TS of a given reaction step more closely resembles the reaction partner (reactant or product) of highest energy." Thus, if a reaction is highly endothermic (or endergonic), the TS tends to more closely resemble the product than the reactant, although it is still a resonance hybride of both. If, on the other hand, a reaction is highly exothermic (or exergonic), the TS tends to more closely resemble the reactant. Traditionally, the Hammond Principle is discussed in terms of enthalpies, that is, endothermicity and exothermicity.

It is important to note that the Hammond Principle helps define the TS for a specific, single reaction step, not the overall reaction. Since we are considering relative rates, the step we are most interested in is the rds, becasuse the rate of the reaction equals the rate of this step. In the addition of HCl to an alkene, this step is quite endothermic. We could, and would be expected to, simply look at this reaction step and predict that it would be endothermic. Remember that two bonds are broken in this reaction and only one formed. It is thus substantially endothermic. As a matter of convenience, it may be well to remember that any time a high energy intermediate such as a carbocation is formed, that reaction step is endothermic. From the Hammond Principle we may then conclude that the TS for this step closely resembles the product (of that step), which is a carbocation. Therefore the TS for the rds of this reaction has very extensive carbocation character.

On the other hand, the final step (which is fast and not rate determining) is highly exothermic, so the TS for that step (reaction of a carbocation with the chloride anion) closely resembles the reactant. By the way, the reactant in this step is also this same carbocation. Therefore the TS for both steps closely resembles the carbocation. Nevertheless, we are presently interested only in the rds (because we are concerned with relative rates).

Consequently, we can predict that rate ratios in the series of alkenes previously considered will be large, and also regiospecificity in the addition to an unsymmetrical alkene will be high, as indeed is the case.

BACK TO THE TOP OF THIS PAGE

BACK TO ALKENES 1

ON TO THE FINAL PART OF ALKENES

BACK TO THE BAULD HOME PAGE